37. Барометрическая формула. Распределение Больцмана.

Молекулы любого газа всегда находятся в поле тяготения Земли. Совместные действия поля тяготения и теплового движения приводят к такому состоянию атмосферы, при котором концентрация и давление газа убывают с возрастанием высоты над Землей.

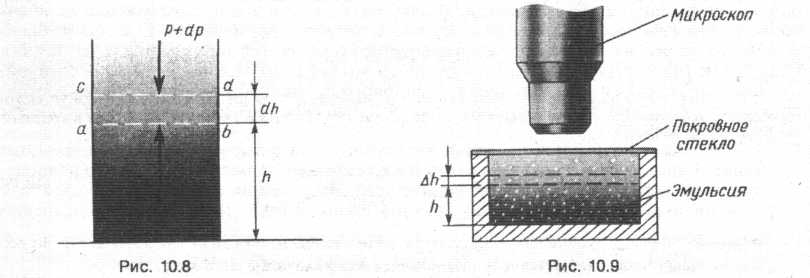
Найдем закон изменения давления идеального газа с высотой в однородном поле тяготения. Будем считать, его температура Т всюду одинакова. Выделим на высоте h столб abcd газа высотой dh и площадью основания, равной единице (рис. 10.8). Разность давлений p и p+dp равна гидростатическому давлению pgdh столба abcd газа:

Заменим в этом уравнении плотность ρ[ро] на pM/RT:

Интегрируя это выражение по высоте от 0 до h и по давлению от p_Q до р, получаем

или

Здесь р₀ давление газа на высоте h= 0. Если с помощью барометра измерить давление р₀ и р, то по формуле (10.16) можно по изменению давления определить высоту:

Поэтому (10.16) называется барометрической формулой. Барометр, специально про­градуированный для отсчета высоты над уровнем моря, называется альтиметром. Он широко применяется в авиации, при восхождениях на горы и т. п.

3. Барометрическая формула позволяет получить соотношение между концентраци­ями газа на различных высотах. Используем уравнение состояния идеального газа в форме: р = п₀кТ, где п₀ концентрация молекул газа. При Т= const имеем

где п₀₀— концентрация молекул газа при давлении р₀(на высоте h = 0). Поэтому уравнение (10.16) можно записать в форме

Заменяя R/M=k/m₀, где m₀ — масса молекулы газа, получаем

Из формулы (10.17') следует, что n₀→n₀₀ при T→∞, т. е. повышение температуры приводит к выравниванию концентрации газа по всему предоставленному ему объему. При T→0 К n₀→0, т. е. молекулы под действием силы тяжести будут опускаться на дно

сосуда. Наша атмосфера существует лишь благодаря тепловому движению частиц воздуха.

Если учесть, что mgh= W_n то формулу (10.17') можно переписать в виде

Значение этого соотношения далеко выходит за рамки рассмотренной нами конк­ретной задачи. Формула (10.18) является математическим выражением весьма общего и важного закона — закона Больцмана для распределения частиц во внешнем потенци­альном поле. Закон Больцмана справедлив для любого потенциального поля независимо от его физической природы.

Заменив в (10.17) M=m₀N_A, получим

Это выражение можно использовать для экспериментального определения одной из важнейших констант физики — постоянной Авогадро:

38. Средняя длина свободного пробега молекул.

Молекулы непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями моле­кулы движутся равномерно и прямолинейно.

Расстояние λ, которое молекула пролетает за время свободного пробега от одного столкновения до следующего, называется длиной свободного пробега. Эти расстояния могут быть самыми разными. Поэтому в кинетической теории вводится понятие средней длины свободного пробега молекул <λ>. Величина <λ> является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.

Для вычисления <λ> необходимо принять определенную модель молекул газа. Будем считать, что молекулы представляют собой шарики некоторого диаметра d порядка 10^-10 м, зависящего от химической природы газа.

Такая модель правильно передает характер сил отталкива­ния, которые действуют при сильном сближении молекул реальных газов.

Подсчитаем среднее число столкновений, которое испытывает за единицу времени молекула при движении в однородном газе. <Z> - среднее число столкновений; d –диаметр молекул; <u> -средняя скорость движения рассматриваемой молекулы(все остальные молекулы неподвижны); n₀ — концентрация молекул газа. Тогда:

В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости Поэтому значение среднего числа соударений нужно увеличить в 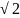раз:

Среднее расстояние, которое пролетает молекула за единицу времени, численно равно <и>. Оно представляет собой произведение <Z> <λ>. средняя длина свободного пробега молекул

Для данного газа при Т = const и различных давлениях р₁ и р₂ имеем

Рассмотрим опыт Борна и Бормана (1921). В этом опыте исследована закономерность убывания интенсивности пучка атомов серебра по мере его распространения в замкнутом сосуде с сильно разреженным воздухом. Пусть N — число атомов, прошедших без рассеяния путь в воздухе, равный х, a |dN| — число атомов, испытыва­ющих столкновения с молекулами воздуха в слое толщиной dx и выбывающих из пучка в этом слое (dN<0). Отношение - dN/N есть вероятность того, что атом серебра, долетевший до рас­сматриваемого слоя, выйдет в этом слое из пучка. Вероятность такого события равна вероятности столкновения атома с молекулой воздуха в слое толщиной dx, т. е. равна отношению dx/<λ>. Таким образом,

Проинтегрировав это уравнение, получим

где No — число атомов в пучке при х→0. Для определения значений N при разных значе­ниях х Борн и Борман использовали метод осаждения атомов серебра на охлаждаемых стеклян­ных пластинках: чем больше N, тем более плотный слой серебра откладывается за одно и то же время экспонирования на стеклянной пластинке, установленной на пути пучка перпендикулярно ему.

Соотношение (10.23) называется законом распределения свободных пробегов. С его помощью можно найти среднюю длину свободного пробега атомов серебра в воздухе.

если то