30. Изоэнтропийный процесс

Изоэнтропийный процесс — тепловой процесс, происходящий при постоянной энтропии.

Условия, при которых тепловой процесс будет изоэнтропийным, можно получить из равенства Клаузиуса для обратимых процессов:  ,

где   — приращение (дифференциал) энтропии, а   — бесконечно малое полученное количество теплоты. Отсюда следует, что из обратимых процессов изоэнтропийным является только обратимый адиабатный процесс.

Из неравенства Клаузиуса для необратимых процессов  ,

следует, что необратимый адиабатный процесс не может быть изоэнтропийным.

Но вообще и при необратимом процессе энтропия системы может сохранять постоянное значение, если вся производимая энтропия сразу удаляется с помощью теплообмена.

Линию на любой термодинамической диаграмме, изображающую изоэнтропийный процесс, можно называть изоэнтропой. Но обычно её называют адиабатой, так как необратимый процесс (в том числе необратимый адиабатный) нельзя корректно изобразить линией на диаграмме.

31. Изотермический процесс

T=const

PV=RTPV=const

A=PdV=(RT/V)*dV

P=RT/V

C_т=(1/)*Q/T

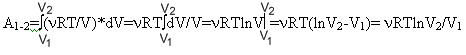
В изотермическом процессе газ ведет себя как система

=m/M

U=0

Q=A

32. Обратимые и необратимые процессы.Энтропия.

1.1 Расширение идеал. газа в пустоту

1.2 Теплообмен между телами

1.3 Адиабатическое расш./сжатие

1.4 Изотермическое расш./сжатие. Квазистатический процесс

Говоря об обратимости,имеем в виду не просто тот факт,что система может быть возвращена в исходное состояние.Задача формулир. шире: в случае обратимого процесса система может быть возвращена в исходное состояние таким образом,что в окружающем мире не произойдет никаких изменений- только в этом случае процесс обратим.

1.1Расширение идеального газа в пустоту

Поскольку газ идеальный и поскольку он не совершает работу над внешними телами в этом случает работа внутренняя- не будет измен. внут. энергии и t газа const.

Водной части объема при числе молекул =N_a

2-ой экспер. по возвращению газа в исх. состояние

Одну из стенок сделаем подвижной

Перемещая правую стенку выдавим газ и вернем систему в исходное состояние.

Газ несколько нагреется,т.к. над ним была совершена работа внешних сил.

Его придется охлаждать,в окруж. мире бедут нагретые тела.

Вывод: процесс расширения идеального газа в пустоту необратим.

1.2 Теплообмен между телами

T₁>T₂

? как сделать так,чтобы T₂ вернуло тепло T₁ и система вернулась в прежнее состояние с помощью холодильной машины.

Вернем наши тела в исходное состояние с помощью холодильной машины.Будем использовать некоторое кол-во идеального газа в цилиндре с подвижным поршнем.

Пусть газ находится в состоянии 1,тогда на 1ом этапе заставим газ расширяться адиабатически до тех пор, пока Т не станет=Т₁

при Т₂ приведем газ в контакт с телом.

участок 3-4

При этом расширяясь изотермически газ заберет у тела некоторое кол-во тепла Q₂

Достигнув точки 3 устраним тепловой контакт рабочего газа с холодным телом,а затем сожмем газ адиабатически, так чтобы его темп. стала=температуре горячего тела(точка 2)

После этого восстановим тепловой контакт газа с горячим телом,будем произв. изотермическое сжатие.

Газ будет отдавать тепло Q₁ горячему телу.Достигнув точки 1,при необх. можем повт. описанный цикл.

Если воспользоваться соотношением |A|=|Q₁-Q₂|

A<0 A= Q₁-Q₂ Q₁= Q₂+|A|

За каждый цикл машина отдает горячему телу тепла>,чем забирает у холодного тела.Это тепло > на величину совершенной газом работы.

Следовательно для того, чтобы вернуть горячее тело в исходное состояние нам придется избыток полученного телом тепла отдать окружающим телам-окр. тела нагреются

Запас мех. энергии,за счет которой совершается работа, уменьшится.

Вывод: мы вернули систему в исходное состояние,но окр. мир изменился(в окр. мире произошли необратимые изменения).

Вывод:процесс необратим.

Теплообмен между телами,имеющими разные температуры-это необратимый процесс.

1.3 Адиабатическое расш./сжатие.

Адиабатный процесс происходит без обмена теплом с окр. телами.

Q=0

Такого вида устройство наз. маховик.

В случае адиабатного процесса и при отсутствии трения такое средство могло бы действовать сколько угодно долго.

При этом газ периодически возвращался бы в исходное положение,а в окр. мире не происходило бы изменений.

Вывод:процесс адиабатического расширения (сжатия)-обратимый процесс.

Если процесс расширения(сжатия) газа происх. медленно,то в этом случае газ будет успевать приходить в тепловое равновесие с теплопередатчиком.

В термодинамике такой бесконечно медленно протекающий процесс называют квазистатическим процессом.

При квазистатическом процессе практически одно равновесное состояние газа сменяется другим.

На любой стадии процесс можно прекратить и повернуть его в обратную сторону.

Происходит передача тепла между системой и тепловым резервуаром при равных t обоих.Такой обмен будет обратимым процессом.

Термодинамическая вероятность.

Реальная система состоит из большого числа частиц.

Любое макросостояние такой системы реализуется большим количеством микросостояний.

В классической физике мы можем различать одну молекулу от другой как они отличны по V и энергии.

Термодинамическая вероятность в термодинамике.

Она зависит от V,доступного частицам объема

N-V WV^N=(VVVV…V) N раз

W-термодинамическая вероятность

Если в 1 систему объединить 2 термодин. сист.(их называют подсистемами),то термодин. вероятность этой системы=произведению вероятностей подсистем

W=W₁*W₂

Очень большие числа были не удобны,и Больцман предложил использовать не саму термодин. вероятность, а ln термодин. вероятности.

Понятие энтропии.

S=klnW

использование такой характеристики более удобно,тк ln от большого числа число небольш.

При объединении систем происходит сложение энтропии.

W=W₁*W₂ S=kln W₁*W₂₌ kln W₁+ kln W₂=S₁+S₂

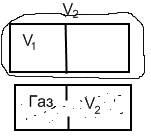
Оценим изм. энтропии,кот. происх. в этом процессе

W₁V₁^N S₁=kNln V₁+const

W₂V₂^N S₂=kNln V₂+const

 S= S₂-S₁=kN(ln V₂- ln V₁)= kNlnV₂ /V₁

lnV^N= Nln V

 S= kNlnV₂ /V₁; Q=A= RT lnV₂ /V₁

N=N_aS=R lnV₂ /V₁

= m/M; N_ak=R

S=Qобр./T

Изотерм. процесс:

S=Q/T

энтропия представляет собой параметр состояния системы.

Энтропия не зависит от путей достижения данного состояния.

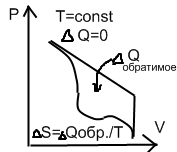
Формула справедлива и при переходе с другими процессами, главное, чтобы они не были необратимыми.