27. Теплоёмкость идеального газа.Теплоёмкость при постоянном объёме и постоянном давлении.Уравнение Майера.

Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

Теплоёмкость ид.газа в изопроцессах:

Адиабатический

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть  . Однако, объём, давление и температура меняются, то есть  .Следовательно, теплоемкость идеального газа в адиабатическом процессе равна нулю:  .

Изотермический

В изотермическом процессе постоянна температура, то есть  . При изменении объема газу передается некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к

бесконечности: 

Изохорный

В изохорном процессе постоянен объем, то есть  . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение ( ). Первое Начало Термодинамики для изохорного процесса имеет вид:

А для идеального газа

Таким образом,

где   — число степеней свободы частиц газа.

Изобарный

В изобарном процессе ( ):

C_P=δQ/νΔT=C_V+R=((i+2)/2)*R

Теплоемкость, как и кол-во тепла, зависит от вида теплового процесса. Различают теплоемкости при постоянном давлении и постоянном объеме. Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщенная газу извне теплота идет на увеличение его внутренней энергии: .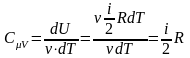

Используя первое начало термодинамики, можно показать, что молярная теплоемкость газа при постоянном объеме C_V и молярная теплоемкость газа при постоянном давлении C_P связаны соотношением

.

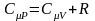Это соотношение называется уравнением Майера.

28. Теплоёмкости одноатомных и многоатомных газов

Теплоёмкости одноатомных газов  С_V  и  С_Р 

где теплоемкость при постоянном объеме С_V – величина постоянная, от температуры не зависит.  Учитывая физический смысл R для изобарических процессов, можно записать:

(для одного моля)

Тогда теплоемкость при постоянном давлении для одноатомных газов:

или

Полезно знать соотношение:

где γ - коэффициент Пуассона, 

Так как  , то  . Из этого следует, что

Кроме того,  , где i – число степеней свободы молекул.  Подставив в выражение для внутренней энергии, получим:

Так как  , то внутреннюю энергию можно найти по формуле

Теплоемкости многоатомных газов  Опыты с двухатомными газами, такими как азот, кислород и др., показали, что

Для водяного пара и других многоатомных газов

Таким образом, молекулы многоатомных газов нельзя рассматривать как материальные точки. Необходимо учитывать вращательное движение молекул и число степеней свободы этих молекул.  Числом степени свободы (i) называется число независимых переменных, определяющих положение тела в пространстве.  Положение одноатомной молекулы, как и материальной точки, задаётся тремя координатами, поэтому она имеет три степени свободы.  Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения, а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомной молекулы вращение вокруг её собственной оси не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю (рис. 4.3).  Таким образом, у двухатомных молекул пять степеней свободы (i = 5), а у трёхатомных шесть степеней свободы (i = 6).При взаимных столкновениях молекул возможен обмен их энергиями и превращение энергии вращательного движения в энергию поступательного движения и обратно. Таким путём было установлено равновесие между значениями средних энергий поступательного и вращательного движения молекул. Больцман доказал, что для не слишком низких температур средняя энергия <K>, приходящаяся на одну степень свободы, равна ½ Kt

29. pv-диаграммы.Изобарный и изохорный процессы

Изобарный

При изобарическом процессе, давление в газе остается неизменным (Δp = 0). Объем идеального газа при изобарном процессе пропорционален температуре V/T=const.

Изобарный процесс можно описать уравнением:

V = V_oαT, где

V – объем газа при абсолютной температуре Т;

V_o — объем газа при температуре 0^оС;

α — температурный коэффициент объемного расширения газа, равный 1/273 К^-1

Работа, совершаемая газом при расширении или сжатии газа, равна A = PΔV.

Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: Q = ΔH = ΔU + PΔV.

Молярная теплоёмкость при постоянном давлении обозначается как C_p. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера

C_p = C_v + R.где

R - универсальная газовая постоянная - R=8.31 (Дж/(моль*К))

Энтропия процесса

Изменение энтропии при квазистатическом (идеализированный процесс, состоящий из непрерывно следующих друг за другом состояний равновесия) изобарном процессе равно:

где

H, H₁, H₂ - энтальпия

dS - изменение энтропии

Изохорный

Изохорный процесс

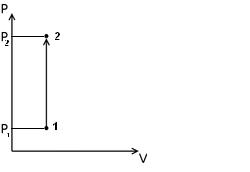
Изохорный процесс происходит при постоянном объёме, при этом давление идеального газа прямо пропорционально его температуре

p/T=const.

Работу в этом процессе газ не совершает (т.к ΔV=0), соответственно Q= ΔU

Уравнение изохорного процесса (уравнение Шарля) может быть записано в виде:

p=Tp₀/T₀=p₀αT где

p₀ – давление газа при T = T₀ = 273 К

α — температурный коэффициент объемного расширения газа, равный 1/273 К^-1

Энтропия процесса

Т.к. в системе при изохорном процессе происходит теплообмен с внешней средой, то, соответственно, происходит изменение энтропии. Из определения энтропии следует:

где

dS - изменение энтропии

dQ - изменение энергии