Следствия из преобразований Лоренца

1. Длина движущегося стержня.

Предположим, что стержень расположен вдоль оси х` в системе k` и движется вместе с системой k` со скоростью v.

Разность между координатами конца и начала отрезка в системе отсчета, в которой он неподвижен, называется собственной длиной отрезка. В нашем случае l₀ = х₂` - х<sub>1</sub>`, где х₂` - координата конца отрезка в системе k` и х/ - координата начала. Относительно системы k стержень движется. Длиной движущегося стержня принимают разность между координатами конца и начала стержня в один и тот же момент времени по часам системы k.

где l - длина движущегося стержня, l₀ - собственная длина стержня. Длина движущегося стержня меньше собственной длины.

2. Темп хода движущихся часов.

Пусть в точке х₀` движущейся системы координат k` происходит последовательно два события в моменты t/ и t₂. В неподвижной системе координат k эти события происходят в разных точках в моменты t₁ и t₂. Интервал времени между этими событиями в движущейся системе координат равен дельта t` = t<sub>2</sub>` - t₁`, а в покоящейся дельта t = t₂ - t₁.

На основании преобразования Лоренца получим:

Интервал времени дельта t` между событиями, измеренный движущимися часами, меньше, чем интервал времени дельта t между теми же событиями, измеренный покоящимися часами. Это означает, что темп хода движущихся часов замедлен относительно неподвижных.

Время, которое измеряется по часам, связанным с движущейся точкой, называется собственным временем этой точки.

3. Относительность одновременности.

Из преобразований Лоренца следует, что если в системе k в точке с координатами x₁ и х₂ происходили два события одновременно (t₁ = t₂ = t₀), то в системе k` интервал

понятие одновременности - понятие относительное. События, одновременные в одной системе координат, оказались неодновременными в другой.

4. Относительность одновременности и причинность.

Из относительности одновременности следует, что последовательность одних и тех же событий в различных системах координат различна.

Не может ли случиться так, что в одной системе координат причина предшествует следствию, а в другой, наоборот, следствие предшествует причине?

Чтобы причинно-следственная связь между событиями имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.

Таким образом, передача физического влияния из одной точки в другую не может происходить со скоростью, большей скорости света. При этом условии причинная связь событий носит абсолютный характер: не существует системы координат, в которой причина и следствие меняются местами.

21. Релятивистский закон сложения скоростей

Новым релятивистским представлениям о пространстве и времени соответствует новый закон сложения скоростей.

Запишем закон сложения скоростей для частного случая, когда тело М движется вдоль оси X' системы отсчета К', которая, в свою очередь, движется со скоростью  υ⃗  относительно системы отсчета К. Причем в процессе движения координатные оси X и X' все время совпадают, а координатные оси Y и Y', Z и Z' остаются параллельными (рис. 18.4).

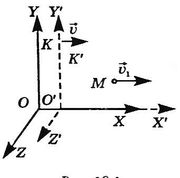
Рис. 18.4

Обозначим модуль скорости тела относительно К' через  υ1 а модуль скорости этого же тела относительно К через  υ2. Тогда релятивистский закон сложения скоростей будет иметь вид

 (18.4)

Заметим, что формула (18.4) применима только в том случае, если все три вектора  υ⃗ ,υ⃗ 1 и  υ⃗ 2 направлены вдоль одной прямой. В общем случае этот закон имеет более сложный вид. Однако при любой форме записи закона его сущность заключается в том, что скорость c света в вакууме является предельной скоростью передачи сигналов.

Действительно, пусть  υ1=c. Найдем скорость  υ2:

Предположим, что тело движется со скоростью  υ1=c относительно системы К', которая в свою очередь движется со скоростью  υ=c относительно системы К. Тогда 

Следовательно, при любых скоростях  υ1 и  υ результирующая скорость  υ2 не превышает с.

Если υ≪c и υ1≪c, то членом  знаменателе можно пренебречь и вместо (18.4) получим классический закон сложения скоростей

 υ₂=υ₁+υ.

Это согласуется с принципом соответствия, согласно которому новая физическая теория не отвергает целиком предшествующую теорию, она указывает предел применимости старой теории. 

Релятивистский закон сложения скоростей: если в неподвижной ситеме отсчета скорость тела и скорость движущейся системы отсчета направлены по одной прямой, то:  

где u ' – скорость движения тела в движущейся системе отсчета; v – скорость движущейся системы K ' относительно неподвижной системы K;  u – скорость тела относительно неподвижной системы отсчета K

22. Следствия из преобразований Лоренца

1. Если в одной системе отсчета некоторые события происходят в точках x₁ и x₂ в один и тот же момент времени t, то в другой системе отсчета эти события происходят в точках x'₁ и x'₂ в разные моменты времени t'₁ и t'₂:

Понятие одновременности оказывается зависящим от выбора системы отсчета.

2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсчета между этими же событиями проходит время

Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах.

3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина

Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциальные системы отсчета.

4. Если в одной системе отсчета тело имеет скорость v = (v_x, v_y, v_z), то его скорость v' = (v'_x, v'_y, v'_z) в другой системе отсчета равна

или в трехмерной векторной форме 

5. Из соотношений (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии v²=(v_x)²+(v_y) ²+(v_z) ²=c², (n6)

получим v'²=(v'_x)²+ (v'_y)²+(v'_z) ²=c². (n7)

Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v' в общем случае различны в разных системах отсчета.

22. Лоренцево сокращение длины.

Рассмотрим рисунок 8.5, на котором изображены две системы координат  k  и  k'.

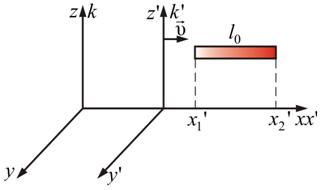  Рис. 8.5

       Пусть  l₀ = x'₂ – x'₂  – собственная длина тела в системе, относительно которого тело неподвижно (например: в ракете, движущейся со скоростью мимо неподвижной системы отсчета  k (Земля)). Измерение координат  x₁  и  x₂  производим одновременно в системе  k, т.е.  t₁ = t₂ = t.

       Используя преобразования Лоренца, для координат получим:

.

       Тогда

(8.4.6)

       Формулы (8.4.6) описывают лоренцево сокращение длин. Собственная длина тела есть максимальная длина. Длина движущегося тела короче, чем покоящегося. Причем сокращается только проекция на ось x, т.е. размер тела вдоль направления движения.

23. Замедление времени. 

Так называемое замедление времени илизамедление хода движущихся часов.Под релятивистским замедлением времени обычно подразумевают кинематический эффект специальной теории относительности, заключающийся в том, что в движущемся теле все физические процессы проходят медленнее, чем следовало бы для неподвижного тела по отсчётам времени неподвижной (лабораторной) системе отсчёта. 

Релятивистское замедление времени проявляется, например, при наблюдении короткоживущих элементарных частиц, образующихся в верхних слоях атмосферы под действием космических лучей и успевающих благодаря ему достичь поверхности Земли.

В качестве иллюстрации релятивистского замедления времени часто приводится парадокс близнецов.

Количественное описание замедления времени может быть получено из преобразований Лоренца: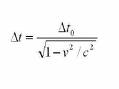 где ?t — время, проходящее между двумя событиями движущегося объекта с точки зрения неподвижного наблюдателя, ?t0 — время, проходящее между двумя событиями движущегося объекта с точки зрения наблюдателя связанного с движущемся объектом, v — относительная скорость движения объекта, c — скорость света в вакууме. Точность формулы неоднократно проверена на элементарных частицах и атомах, так что относительная ошибка составляет менее 0,1 ppm.