1. Кинематика материальной точки.

Кинематика-это раздел изучающий движение тел без влияния других тел, описывает движения тел, скорость, ускорение, но не отвечает на вопрос почему движется тело.

Матер.точка-это тело формой и размерами которого можно пренебречь.(имеет массу но не имеет размера).

Движение всегда относительное. Нужно выбирать тело отсчета. С телом отсчета связана система координат и она снабжается часами.

В инерциальной системе отсчета выполняются законы Ньютона.

Координатный способ движения материальной точки.

Положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=x(t), y=y(t), z=z(t).

Приведенные три зависимости задают траекторию в параметрической форме. В ряде случаев можно исключить параметр t выразив t подставив в другое уравнение.

Векторный способ описания движения материальной точки

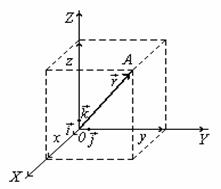
Радиус вектор-вектор, проведенный из одной точки к точки пространства.

Орты-вспомогательные векторы, которые определяют направление координатных осей.

Введем три единичных вектора, орты , направленных вдоль осей X, Y, Z, соответственно. Тогда, как видно из рисунка, , а модуль радиус–вектора равен .

Путь и перемещение.

Расстояние которое проходит материальная точка называется пройденный путь, это скалярная величина. Пройденный путь измеряется в направлении движения точки. Пройденный путь неубывающая функция времени.

Вектор перемещения это вектор из начала в точку конечного перемещения. Если мат.точка возвращается в начало то вектор перемещения равен 0.

2. Скорость и ускорение

Скорость-векторная величина.

Средняя путевая скорость-величина отношения пути который проходит точка к еденице времени

. М/С.

Средняя скорость перемещения-грубо характеризует материальную точку.

Мгновенная скорость

Вектор мгновенной скорости направлен по касательной к траектории движения материальной точки.

Быстроту изменения скорости характеризует физическая величина, называемая уско-

рением. Поскольку скорость v является функцией времени, ускорение может быть представлено как производная скорости по времени:

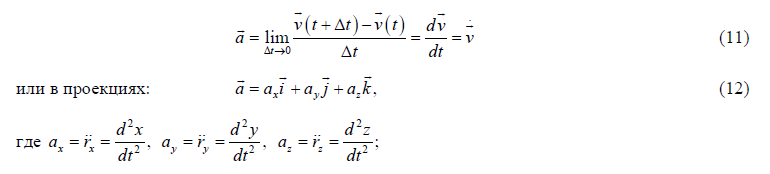
Естественный способ описания движения

При этом произвольно выбирают положительное направление отсчета координаты l .

Движение частицы задано полностью, если определена ее траектория, начало отсчета О, положительное направление отсчета дуговой координаты l и закон движения частицы, т. е. зависимость .

Рассмотрим как в этом способе описания определяется скорость частицы. Введем единичный вектор , связанный с движущейся точкой А и направленный по касательной к траектории в сторону увеличения дуговой координаты l Ясно, что - переменный вектор: его направление зависит от l, хотя длина этого вектора остается неизменной. Вектор скорости частицы А направлен по касательной к траектории, поэтому его можно выразить так: