30.Теорема о перпендикулярности прямой и плоскости

Терема.Если прямая перпендикулярна к плоскости в пространстве, то на комплексном чертеже горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция перпендикулярна к фронтальной проекции фронтали, принадлежащим этой плоскости. Пусть прямая (АК) перпендикулярна к плоскости общего положения   (рис. 4.13). Проведем в плоскости   произвольные горизонталь h и фронталь f. Так как перпендикуляр к плоскости образует прямые углы со всеми прямыми, принадлежащими плоскости, то (АК)   h и (АК)  f.  Р 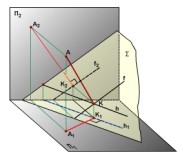ис. 4.13

На основании теоремы 1:  1) прямой угол АКh проецируется на плоскость П₁ без искажения, т. е.  (А₂К₂)   h, так как h  П₁; 2) прямой угол АКf проецируется на плоскость П₂ без искажения, т. е. (А₂К₂)   f₂, тах как f   П2. Напомним, что все горизонтали, принадлежащие одной и той же плоскости, параллельны между собой, а все фронтали между собой. Поэтому для построения проекций перпендикуляра к плоскости можно воспользоваться любыми горизонталью и фронталью, принадлежащими плоскости.