
- •§ 1. Вероятностное пространство
- •Упражнения
- •§ 2. Случайные величины.
- •Упражнения.
- •§ 3. Основные понятия теории надежности.
- •Упражнения.
- •§ 4. Статистическое оценивание показателей надежности.
- •Упражнения.
- •§ 5. Показатели надежности для сложных систем.
- •Упражнения.
- •§ 6. Гамма-функция и ее свойства.
- •Упражнения
- •§ 7. Некоторые законы распределения времени наработки на отказ.
- •Упражнения.
- •§ 10. Гамма - распределение.
- •Упражнения.
- •Приложение 2. Ргр Законы распределения времени наработки на отказ.
- •Литература
Упражнения
6.1.
Вычислить 1)
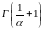 ;
2)
;
2)
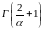 ,
если а)
,
если а)
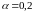 ;
б)
;
б)
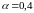 .
.
6.2. Проверить справедливость формулы
 при
при
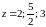 .
.
6.3.
Вычислить а)
 ,
б)
,
б)
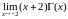 ,
и)
,
и)
 .
.
Ответ: а)
– 1; б)
;
в)
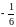 .
.
§ 7. Некоторые законы распределения времени наработки на отказ.
7.1. Экспоненциальный закон . Подробно рассмотрен в §§ 2, 3.
 .
.

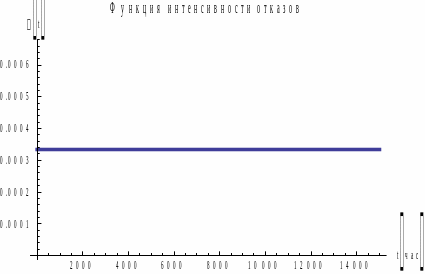

Рис. 2. Графики
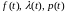 для
для
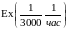 .
.
7.2.
Нормальный закон
 .
Подробно рассмотрен
в §§ 2, 3.
.
Подробно рассмотрен
в §§ 2, 3.
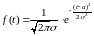 ,
,
,
,
;
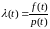 ;
;
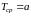 .
.
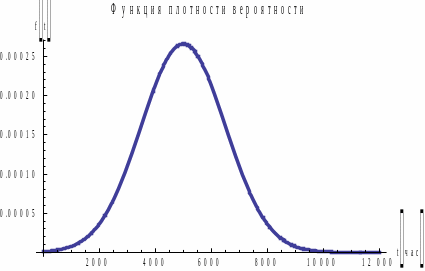
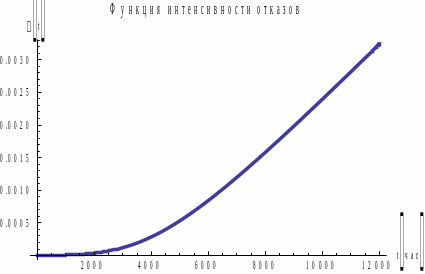
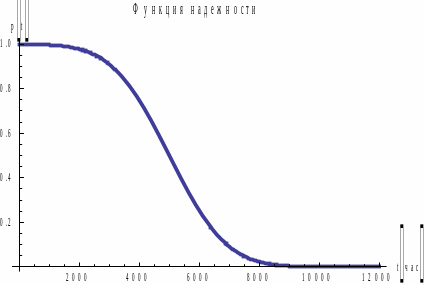
Рис. 3.
Графики
для распределения
 .
.
7.3.
Распределение Рэлея
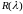 .
.
Определение 1. Случайная величина Т называется распределенной по закону Рэлея , если ее функция распределения
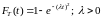 – параметр
распределения. (1)
– параметр
распределения. (1)
Замечание.
 – функция надежности, (2)
– функция надежности, (2)
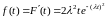 – функция
плотности распределения вероятностей, (3)
– функция
плотности распределения вероятностей, (3)
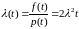 – функция
интенсивности отказов. (4)
– функция
интенсивности отказов. (4)
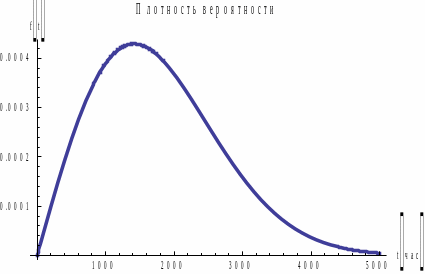
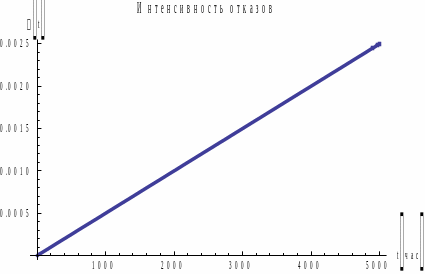

Рис. 4. Графики
для
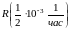 .
.
График в распределении прямо пропорционально зависит от t. Поэтому этот закон применяют для исследования систем с ярко выраженным эффектом старения.
Так как
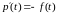 ,
то точка локального максимума для
функции
,
то точка локального максимума для
функции
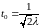 будет точкой перегиба для функции
будет точкой перегиба для функции
 .
.
Найдем еще
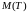 и
и
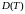 .
По формуле (9) § 3
.
По формуле (9) § 3
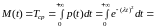
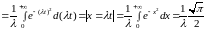 ,
так как
,
так как
 - интеграл Пуассона.
- интеграл Пуассона.
Таким образом
 . (5)
. (5)
По формуле (10) § 3


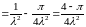 .
.
Таким образом
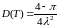 . (6)
. (6)
Пример
1. Время Т
наработки системы на отказ распределено
по закону
.
При этом интенсивность отказов
при t=1000
час
равна:
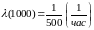 .
.
Найти: 1) вероятность безотказной работы системы в течение 500 час;
2)
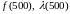 ;
;
3) .
Решение.
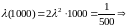
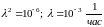 .
Тогда 1)
.
Тогда 1)
 .
.
2)
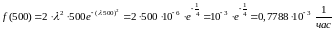

3)
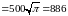 час.
час.
7.4. Распределение Вейбулла.
Определение
2. Случайная
величина Т называется распределенной
по закону Вейбулла
 ,
если ее функция распределения
,
если ее функция распределения
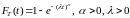 - (7)
- (7)
параметры
распределения,
 .
.
Замечание.
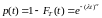 - функция надежности, (8)
- функция надежности, (8)
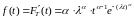 - (9)
- (9)
функция плотности распределения вероятностей,
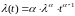 - функция интенсивности отказов. (10)
- функция интенсивности отказов. (10)
При
 становится экспоненциальным распределением
.
становится экспоненциальным распределением
.
При
 становится распределением Рэлея
.
становится распределением Рэлея
.
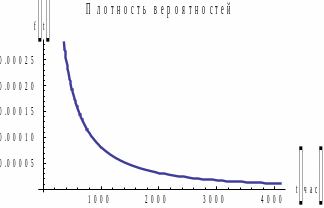
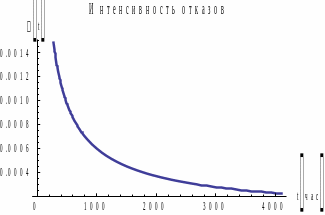
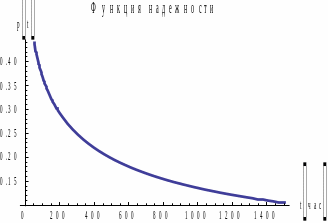
Рис.
5.
Графики
для распределения
 .
.
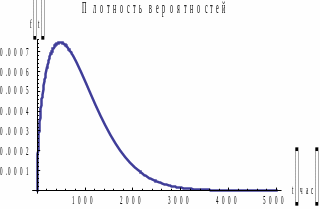

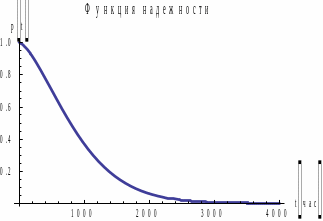
Рис.
6.
Графики
для распределения
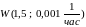 .
.


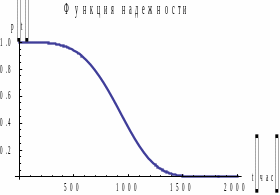
Рис.
7.
Графики
для распределения
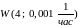 .
.
Найдем М(Т) и D(Т)
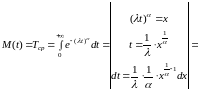
 .
.
Таким образом
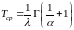 . (11)
. (11)
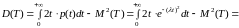

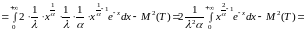
 .
.
Таким образом
 . (12)
. (12)
Пример
2. Время Т
наработки системы на отказ распределено
по закону Вейбулла
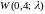 .
При этом интенсивность отказов
в момент времени t=1000
час
равна
.
При этом интенсивность отказов
в момент времени t=1000
час
равна
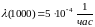 .
Найти :
.
Найти :
1) вероятность безотказной работы за это время.
2) .
Решение. 1) По Формуле (10):
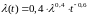 ;
;
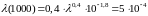 ;
;
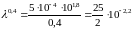 .
.
По формуле (8):
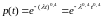 .
.
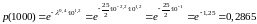 .
.
2) По формуле (11):
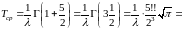
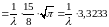 .
.
Так как
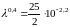 ,
то
,
то
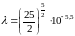 и
и
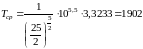 час.
час.
Упражнения.
7.1.
Нерезервированная
невосстанавливаемая система состоит
из 3-х последовательно соединенных
элементов. Время жизни элементов
распределено по закону Рэлея:
 .
Определить показатели надежности
системы:
.
Определить время, в течение которого
система будет исправна с вероятностью
.
.
Определить показатели надежности
системы:
.
Определить время, в течение которого
система будет исправна с вероятностью
.
Ответ.
 ,
,
 .
.
7.2.
Нерезервированная
система состоит из n
последовательно соединенных элементов,
время жизни которых
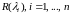 .
1) Найти показатели надежности системы.
2) Определить по какому закону распределено
время жизни системы.
.
1) Найти показатели надежности системы.
2) Определить по какому закону распределено
время жизни системы.
Ответ.
1)
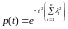
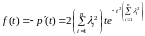 ;
;
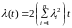 .
.
2)
 .
.
7.3.
Резервированная
невосстанавливаемая система состоит
из 2-х параллельно соединенных элементов
(постоянно включенный резерв). Время
жизни каждого элемента
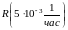 .
Определить показатели надежности
системы:
.
Определить
для
одного элемента.
.
Определить показатели надежности
системы:
.
Определить
для
одного элемента.
Ответ.
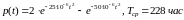 ,
,
Тср(для одного элемента) = 177 час.
7.4.
Время Т
наработки элемента на отказ распределено
по закону Вейбулла
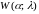 .
При этом интенсивность отказов
:
.
При этом интенсивность отказов
:
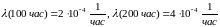 .
Найти :
.
Найти :
1) Найти параметры
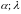 .
.
2) Найти показатели надежности при t=2000 час.
3) , D(T).
Ответ.
1)
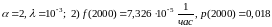 ,
,
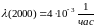 ;
3)
;
3)
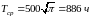 ,
,
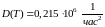 .
.
7.5.
Нерезервированная система состоит из
8 последевательно соединенных элементов,
время жизни которых распределено по
закону
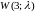 .
Определить по какому закону распределено
время жизни системы.
.
Определить по какому закону распределено
время жизни системы.
Ответ.
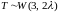 .
.
7.6.
Время Т
наработки детали на отказ распределено
по закону Рэлея
.
Найти показатели надежности работы
детали
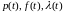 при а) t=10000
час, б) t=20000
час. Найти
,
D(T).
при а) t=10000
час, б) t=20000
час. Найти
,
D(T).
7.7.
Время Т
наработки системы на отказ распределено
по закону
,
при этом интенсивность отказов
при t=5000
час равна:
 .
Найти 1)
параметр
;
2)
,
D(T);
3) показатели надежности работы системы
а) через год, б) через 2 года ( считать,
что в году 8760 час).
.
Найти 1)
параметр
;
2)
,
D(T);
3) показатели надежности работы системы
а) через год, б) через 2 года ( считать,
что в году 8760 час).
7.8.
Нерезервированная
система состоит из 2-х последовательно
соединенных элементов. Время жизни
1-ого элемента распределено по закону
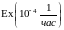 ,
2-ого -
.
Найти 1) показатели надежности системы,
2)
.
,
2-ого -
.
Найти 1) показатели надежности системы,
2)
.
7.9.
Время Т наработки элемента на отказ
распределено по закону Вейбулла
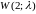 .
При этом интенсивность отказов
.
При этом интенсивность отказов
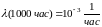 .
.
1) Найти параметр
 .
.
2) Найти показатели надежности через t=2000 час.
3) .
Ответ.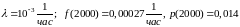 ,
,
 ;
;
 .
.
7.10.
Время Т
наработки устройства на отказ распределено
по закону
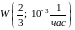 .
Найти Тср
, D(T),
показатели надежности через t=2000
час.
.
Найти Тср
, D(T),
показатели надежности через t=2000
час.
Ответ.
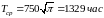 ;
;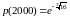 ,
,
 ;
;
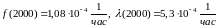 ,
,
