Упражнения.

5.1. Нерезервированная невосстанавливаемая система состоит из 3-х последовательно соединенных элементов. Время жизни элементов экспоненциальное: , , . Определить показатели надежности системы: . Определить время, в течение которого система будет исправна с вероятностью .

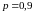5.2. Резервированная невосстанавливаемая система состоит из 2-х параллельно соединенных элементов (постоянно включенный резерв). Время жизни каждого элемента . а) Определить показатели надежности системы: . б) определить выигрыш в надежности , , при t=2000 час.

Ответ: а) ,

,

,

.

5.3. Нерезервированная система состоит из 2-х последовательно соединенных элементов. Время жизни каждого 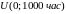. Найти показатели надежности системы. Найти .

5.4. Невосстанавливаемая система состоит из 2-х параллельно соединенных элементов. Время жизни каждого . Найти показатели надежности системы. Найти .

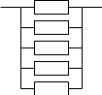
5.5. Система состоит из пяти параллельно соединенных элементов. Время наработки на отказ каждого : 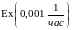. а) Для нормальной работы системы необходимо, чтобы работали хотя бы 3 из 5 элементов:

0. у.

0. у.

0.у. (резерв кратности ).

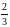1

2

б) Для нормальной работы системы необходимо, чтобы работали хотя бы 4 из 5 элементов:

0. у.

0. у.

0.у. (резерв кратности ).

0. у.

1

Пусть Т – время наработки на отказ системы. Написать формулы для p(t), f(t).

5.6. Время наработки элемента на отказ 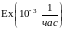. Определить кратность его резервирования такими же элементами, чтобы вероятность безотказной работы системы в течение t=1500 час была 0,9.

Ответ: 9.

5.7. Рассмотрим резервированную систему (резерв замещения кратности 1)

а) Найти показатели надежности.

б) определить выигрыш в надежности , , при t=2000 час.

5.8. Система состоит из трех параллельно соединенных элементов. Время наработки на отказ каждого : . Для нормальной работы системы необходимо, чтобы работало хотя бы 2 элемента из 3-х:

1

2

3

а) Найти показатели надежности.

б) определить выигрыш в надежности при сравнении ее с системой

§ 6. Гамма-функция и ее свойства.

Определение 1. Несобственный интеграл

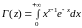, (1)

где , называется эйлеровым интегралом 2-ого рода, а функция переменной z называется гамма-функцией Эйлера. При этом функция

(2)

называется неполной гамма-функцией.

Замечание. Проинтегрируем по частям интеграл (1)

.

Таким образом

. (3)

Т. к. , то из формулы (3) следует: , …

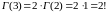
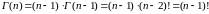
Таким образом 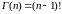(4)

Еще одно соотношение для функции :

. (5)

Поэтому при получим:

.

Далее, используя формулу (3), получим:

.

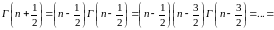
То есть 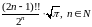. (6)

Замечание. Перепишем формулу (3) в виде

, (7)

что позволяет доопределить функцию для отрицательных значений z.

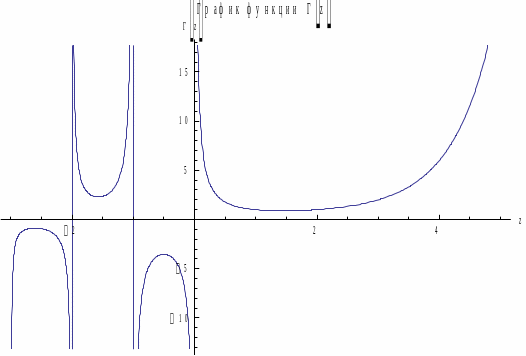
Рис.1 График функции Г(z).

Пример 1. Найти .

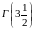Решение. По формуле (6):

= .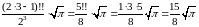