Упражнения.

2.1. Электронная система в состоянии выполнить свои задания при как min четырех исправных каналах из 5 имеющихся. Вероятность P работы каждого канала в течение времени t равна 0,8. Найти вероятность того, что

1) система будет работать;

2) система откажет.

Ответ 2.1: 1) 0,73728, 2) 0,26272.

2.2. Система имеет 4 резервных элемента. Вероятность р отказа каждого из них в течение времени t равна: р=0,25. Найти вероятность того, что в течение времени t будет исправен

1) один элемент;

2) хотя бы один элемент;

3) откажут все;

4) найти среднее число отказных элементов.

Ответ 2.2: 1) 0,046875; 2) 0,9961; 3) 0,0039.

2.3. Устройство состоит из 4 независимо работающих элементов. Вероятность того, что за время t откажет хотя бы один из них равна 0,5904. Найти вероятность того, что за это время откажут:

1) 2 элемента;

2) менее 2-х;

3) не менее 2-х;

4) найти среднее число отказавших элементов.

Ответ 2.3: 1) 0,1536; 2) 0,8192; 3) 0,1808; 4) 0,8.

2.4. Радиосхема состоит из 2000 узлов. Вероятность р отказа любого из них за время t равна: р=0,001. Найти вероятность того, что за время t в системе произойдет:

1) 3 отказа;

2) менее 3-х отказов;

3) не менее 3-х отказов;

4) хотя бы один отказ;

5) найти средне число отказавших элементов.

Ответ 2.4: 1) 0,180447; 2) 0,67667; 3) 0,32333; 4) 0,864665.

2.5. Время Т жизни элемента распределено по закону .

1) Написать функцию распределения и функцию плотности вероятностей 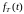для СВ Т.

2) Определить вероятность того, что элемент будет в рабочем состоянии через а) 500 час; б) 1000 час.

3) Определить вероятность того, что время жизни лежит в промежутке .

4) Определить среднее время жизни.

5) Определить вероятность того, что наработка на отказ элемента < 1000 час, при условии, что до 500 часов он работал нормально.

6) Определить какое время наработки на отказ можно гарантировать с вероятностью p=0,6.

Ответ 2.5: 2а) 0,99; 2б) 0,9801; 3) 0,00995; 4) 50000 час; 5) 0,01005; 6) 25541 час.

2.6. Время Т жизни элемента распределено по закону N (2000 час; 500 час).

1) Написать функцию распределения и функцию плотности вероятностей для СВ Т.

2) Определить вероятность того, что элемент будет в рабочем состоянии через а) 2000 час; б) 3000 час.

3) Определить вероятность того, что наработка на отказ лежит в промежутке .

4) Определить среднее время жизни.

5) Определить вероятность того, что время жизни элемента < 3000 час, при условии, что до 2000 часов он работал нормально.

6) Определить какое время жизни можно гарантировать с вероятностью p=0,6.

Ответ 2.6: 2а) 0,5; 2б) 0,0228; 3) 0,4772; 4) 2000 час; 5) 0,9544; 6) 1875 час.

2.7. Конструкторское бюро разрабатывает прибор, рабочий ресурс которого равен a) 7000 час; b) 9000 час; c) 12000 час. При разработке можно использовать одну из четырех деталей А, В, С, D. Время наработки на отказ деталей А, В, С, D распределено соответственно по законам Какую из деталей предпочтительней использовать? Расположить детали в порядке убывания предпочтения.

Ответ 2.7. а) D, C, B, A, b) C, B, A, D, c) B, C, A, D.