Министерство образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Высшая математика № 2»

ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ

НАДЕЖНОСТИ УСТРОЙСТВ И СИСТЕМ

лекции

М и н с к 2 0 12

УДК 519.85 (075.8)

ББК 18.87я7

М 54

Составители: А.Н. Рудый

Рецензенты:

В.В. Карпук, В.В.Павлов

© БНТУ, 2012

§ 1. Вероятностное пространство

Определение 1. Вероятностным пространством будем называть тройку 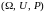, где Ω - пространство элементарных исходов, U – алгебра событий, P – вероятность (функция на U со значениями во множестве действительных чисел R).

Замечание. Ω – это произвольное множество, U – алгебра событий (совокупность подмножеств множества Ω, замкнутая относительно операций сложения, умножения и разности событий ). Свойства функции P:

1)

2)

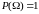
3) 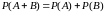– для несовместных событий ( события А и В несовместны, если если произойдет А , то это исключает, что произойдет В, и наоборот).

Определение 2. События А и В независимы, если

. (1)

Определение 3. Пусть 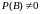. Тогда условная вероятность наступления события А при условии, что В произошло . (2)

Пример 1. Вероятность отказа каждого элемента электрической цепи

M N K

A B

E F

равна 0,1. Элементы работают независимо друг от друга. Отказ элемента – его деструкция, приводящая к разрыву соответствующего участка цепи. Найти вероятность того, что между точками А и В будет идти электрический ток.

Решение. Схема в примере – это логическая модель надежности. При последовательном соединении элементов модели удобно вычислять вероятность работы соответствующего участка (произведение вероятностей работ каждого элемента), при параллельном – отказ (произведение вероятностей отказов каждого элемента).

;

; .

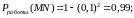
Замечание. При построении логической модели надежности каждому элементу реальной электрической цепи ставят в соответствие элемент логической модели. При этом, если элемент электрической цепи работоспособен – то ему соответствует элемент логической модели, имеющий бесконечную проводимость, а неработоспособному элементу соответствует элемент с нулевой проводимостью.

Например, электрической цепи с диодами

D₁ D₂ D₃

или резисторами

R₁ R₂ R₃

при отказах типа «обрыв», соответствует логическая модель

1 2 3 .

Для конденсаторов можно рассматривать два типа отказов: короткое замыкание или обрыв. Тогда имеет место следующие соответствия электрической цепи и логических моделей.

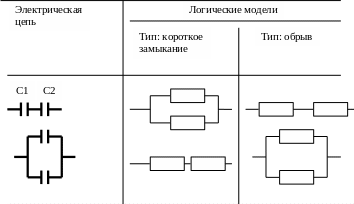
1

1 2

С₁ 2

1

1 2

С₂ 2

Пример 2. Построить логическую модель и определить вероятность безотказной работы схемы соединения конденсаторов.

Типы отказов конденсаторов:

1) короткое замыкание;

2) обрыв.

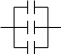
с₁

с₂

с₃

Вероятность безотказной работы каждого .

Решение. 1) Логическая модель надежности:

А В

1 2 3 .

.

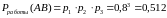2) Логическая модель надежности:

1

A 2 В

3

.

.

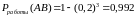Пример 3. Найти вероятность безотказной работы схемы, логическая модель которой:

1 2

5 .

3 4

Вероятность безотказной работы каждого элемента .

Решение. Пусть 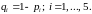Применим метод разложения относительно особого элемента: пусть гипотеза 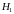- 5-й элемент отказа, 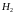- 5-й элемент работоспособен.

.

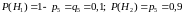Этим гипотезам соответствуют схемы:

1 2

A В .

3 4

1 2

А В

3 4

.

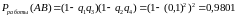Далее по формуле полной вероятности:

.
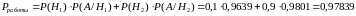