4. Типовые элементарные звенья и их характеристики.

Последовательное соединение звеньев показано на рис. 1.8, 1.9.

Рис. 1.8. Блок-схема последовательного соединения

Рис. 1.9. Граф последовательно соединения

Можно сжать структуру приведенной схемы до одного эквивалентного оператора. Используя операторы соотношения, получим

x₄(p) = W₃(p)x₃(p) = W₃(p)W₂(p)x₂(p) = W₃(p)W₂(p)W₁(p)x₁(p).

Тогда для последовательного соединения звеньев имеем эквивалентную передаточную функцию

. (1.145)

Параллельное соединение звеньев показано на рис. 1.10.

Так как сигналы на выходе всех k звеньев складываются, то результирующая (эквивалентная) передаточная функция равна

. (1.146)

Рис. 1.10. Блок-схема параллельного соединения звеньев

Соединения звеньев с обратной связью приведено на рис. 1.11.

Рис. 1.11. Блок-схема соединения звеньев с обратной связью

Для сигналов, показанных на схеме с отрицательной обратной связью, можно записать следующие соотношения:

x₂ = x₁ – x₂;

x₄ = W₂(p)x₃;

x₂ = W₁(p)x₂.

Исключив промежуточные переменные x₂, x₄, получаем эквивалентную передаточную функцию системы

. (1.147)

При положительной обратной связи (x₂ = x₁ + x₄) имеем

. (1.148)

5. Типовые нелинейности.

(3.1)

а)

Б

(3.2)

)

(3.3)

в)

(3.4)

г)

(3.5)

д)

Однозначные статические нелинейности: а – с насыщением; б – с зоной нечувствительности; в – линейные по модулю; г – идеальная релейная; д - релейная с зоной нечувствительности.

Существуют также петлевые гистерезисные нелинейности (рис. 3.2).

(3.6)

а)

(3.7)

б)

Рис. 3.2. Петлевые гистерезисные характеристики: а – релейная; б – релейная с зоной нечувствительности.

6. Преобразование структурных схем линейных непрерывных систем.

Операция	Исходная схема		Эквивалентная схема
1	2		3
Перенос узла с выхода на вход звена
Перенос узла с входа на выход звена
Перенос сумматора с выхода на вход звена
Перенос сумматора с входа на выход звена
Переход к единичной обратной связи

7. Критерий устойчивости непрерывных линейных систем.

Алгебраические критерии представляют математическое выражение необходимых и достаточных условий отрицательности вещественных частей всех корней уравнения n-й степени с постоянными вещественными коэффициентами

A(p) = a₀pⁿ + a₁p^n1 + _… + a_n1p + a_n = 0. (1.170)

Условия устойчивости линейных систем выражаются с помощью алгебраических неравенств, содержащих значения коэффициентов уравнения (1.170). Они позволяют установить положение корней полинома A(p) в комплексной плоскости p =  + j относительно мнимой оси без вычисления значений корней.

П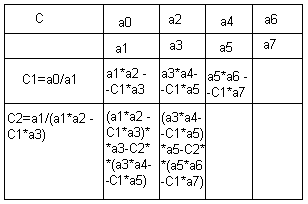 ри работе с полиномом (1.170) будем его приводить к виду, когда a₀ > 0.