1. Математическое описание сигналов в непрерывных линейных детерминированных системах.

При анализе прохождения сложного сигнала U(t) через такие системы его представляют в виде взвешенной суммы базисных функций φ_k(t) (или соответствующего интеграла)

, tt_, t_, (1.1)

где С_k – коэффициенты; t_, t_ – интервал существования сигнала. На интервале t_, t_ выражение справедливо как для сигналов, неограниченных во времени, так и для сигналов конечной длительности.

Вычисление составляющих сигнала существенно облегчается при выборе в качестве базиса системы функций ₀(t), ₁(t),…, _k(t),…, _j(t),…, _n, которую называют ортогональной на отрезке t_, t_ для всех 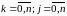, если удовлетворяются условия

при k  j, (1.2)

и ортонормированной, если

при k = j. (1.3)

Распространенной временной формой представления сигнала является такое разложение сигнала U(t), при котором в качестве базисной функции используются единичные импульсные функции – дельта-функции.

Математическое описание такой функции задается соотношениями, когда дельта-функция отличается от нуля в момент времени t = , имеем:

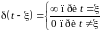; (1.5)

.

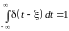Такая математическая модель соответствует импульсу бесконечно малой длительности и безграничной величины. С помощью дельта-функции можно выразить значение реального сигнала U(t) в конкретный момент времени :

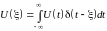. (1.6)

Равенство (1.6) справедливо для любого текущего момента времени t.Заменив  на t и приняв в качестве переменной интегрирования , получим

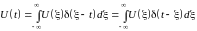. (1.7)

Формула (1.7) справедлива и для более узкого диапазона пределов интегрирования. Так, для любого  > 0 имеем

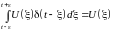. (1.8)

На практике еще пользуются импульсной -функции. При условии, что U(t) имеет непрерывные производные до n-го порядка, с учетом производных -функции имеем

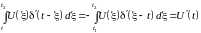(1.9)

и аналогично

(1.10)

при k = 1, 2,…, n.

Единичную импульсную -функцию можно представить прямоугольным импульсом конечной длительности Δ, имеющим единичную площадь в виде рис. 1. Тогда можно записать, что

. (1.11)

Представим интегралом Фурье единичный прямоугольный импульс _(t), определяемый формулой (1.11).

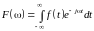(1.12

П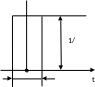 одставляя в (1.14) выражение (1.13) прямоугольно-го импульса, будем иметь

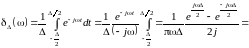
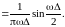(1.13)

Выполнив обратное преобразование Фурье для (1.15), получим

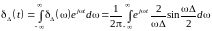. (1.14)

Переходя к пределу при Δ→0 и принимая во внимание, что при этом , получим

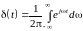. (1.15)

Эта формула дает разложение мгновенного единичного импульса на гармонические колебания всех возможных частот.

Можно подставить выражение (1.17) в формулу (1.7), что позволяет сказать о возможности использования экспоненциальных функций в качестве базисных для сигнала системы.

Использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными парами (с положительным и отрицательным параметром ) позволяет в соответствии с формулой Эйлера

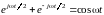(1.16)

представить сложный детерминированный сигнал в виде суммы гармонических составляющих. Поскольку параметр  в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.