1. Фотоэффект. Определения, законы.

Фотоэффе́кт — это испускание электронов веществом под действием света (видимого / инфракрасного / ультрафиолетового / другого электромагнитного излучения). В твёрдых и жидких веществах выделяют внешний и внутренний фотоэффект.

Внешний Ф.Э. – выбитые электроны выходят за пределы освещаемого вещества.

Внутренний Ф.Э. – выбитые электроны остаются внутри освещаемого вещества в качестве «свободных электронов», увеличивая тем самым его электропроводность.

1-й закон: Сила фотоТока прямо пропорциональна плотности светового потока.

2-й закон: Максимальная кинетическая энергия выбиваемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.

3-й закон: Для каждого ве-ва существует красная граница фотоэффекта – минимальная частота света ʋ₀ (или максимальная длинна волны λ₀), при которой ещё возможен фотоэффект, и если ʋ<ʋ₀, то фотоэффект уже не происходит.

Теоретическое объяснение: электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hʋ каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода A_out, покидает металл: hʋ=A_out+W_e, где W_e=mv²/2 — кинетическая энергия, которую имеет электрон при вылете из металла.

2. Комптоновское рассеивание.

Эффект Комптона (Комптон-эффект) – явление изменения длины волны электромагнитного излучения вследствие упругого рассеивания его электронами; Обнаружен Артуром Комптоном для рентгеновского излучения.

При рассеянии фотона на покоящемся электроне частоты фотона ʋ и ʋ’ (до и после рассеяния соответственно) связаны соотношением: ʋ’=ʋ/(1+(hʋ/m_ec²)*(1-cosӨ)), где Ө – угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн: Δλ=λ’-λ=λ_k*(1-cosӨ), где λ_k=h/m_ec – комптоновская длина волны электрона. Для электрона λ_k=2,4263*10^-12(м).

Уменьшение энергии фотона после комптоновского рассеяния – комптоновский сдвиг. В классической электродинамике рассеяние электромагнитной волны на заряде (Томсоновское рассеяние) не сопровождается уменьшением её частоты.

Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны (подтверждает существование фотонов).

Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.

3. Соотношение неопределенности Гейзенберга.

Соотношения неопределённостей Гейзенберга – теоретический предел точности одновременных измерений 2-х характеризующих квантовую систему физических наблюдаемых, описываемых некоммутирующими (не могут быть одновременно точно измерены) операторами (например, координаты и импульса); Задает нижний предел для произведения среднеквадратичных отклонений 2-х квантовых наблюдаемых.

Соот-ие Гейз-а в квантовой механике в математическом смысле – непосредственное прямое следствие некоего свойства преобразования Фурье.

Если имеется несколько (много) идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности – это фундаментальный постулат квантовой механики.

Измеряя величину среднеквадратичного отклонения ΔX координаты и среднеквадратического отклонения ΔP импульса: ΔX*ΔP≥ħ/2, ħ=h/2π, где ħ – приведенная постоянная планка.

В некоторых случаях «неопределённость» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случае нормального распределения переменных, приводит для произведения неопределённостей к большей нижней границе ħ.

Это неравенство даёт несколько возможностей — состояние может быть таким, что X может быть измерен с высокой точностью, но тогда P будет известен только приблизительно, или наоборот P может быть определён точно, в то время как X — нет. Во всех же других состояниях и X, и P могут быть измерены с «разумной» (но не произвольно высокой) точностью.

4. Корпускулярно-волновой дуализм Де’Бройля.

Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные св-ва.

E=ħω, p=ħk, k=2π/λ, λ=с*ʋ, mV²/2=p²/2m=q_eu→p=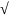 (2mq_eu).

«На деле» квантовые объекты не являются ни классическими волнами, ни классическими частицами, приобретая свойства первых или вторых лишь в некотором приближении – В любом эксперименте проявляются ЛИБО корпускулярные:

Фотоэффект [1], комптоновское рассеяние [2],

давление света – изменение импульса фотона при взаимодействии p=h/λ, Δp=2h/λ, F_давл=Δp/Δt=2h/λΔt, N=E_ф*n=h*(c/λ)*n.

рождение электрон-позитрон(-ых) пар ʋ~10²⁰Гц, E_{ɤ-квант}=hʋ=2m₀C².

ЛИБО волновые свойства:

Интерференция – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн.

дифракция – огибание препятствия волнами. d*sinφ=m_d.

5. Волновая функция, её физический смысл, свойства. Стационарное уравнение Шредингера.

Волновая (пси-) функция [Ѱ] – комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному).

(-ħ²/2m)*▼²*Ѱ+u*Ѱ=i*ħ*(dѰ/dt), где i – мнимая единица, ▼² – оператор Лапласа, u – градиент от координат.

Физический смысл: согласно копенгагенской интерпретации квантовой механики плотность вероятности ω нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной |Ѱ-ии|²  этого состояния в координатном представлении.

dP=A*|Ѱ|²*dV, где А – коэф-т пропорц-ти, dP – вероятность обнаружения частицы в объеме dV. ʃdP=1.

Свойства:

Стандартные условия:

Ѱ-однозначна, непрерывна и конечна; Непрерывны и её производные вероятность обнаружения частицы в элементе объемом dV: dω=|Ѱ|²*dV=Ѱ*Ѱ*dV.

Условия нормировки Ѱ-ии:

Решения удовлетворяют условиям не при любых значениях энергии E, а лишь при некоторых избранных – собственных значениях энергии; Соответствующие им Ѱ-ии – собственные функции: 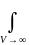(|Ѱ|²*dV=1).

Уравнение Шреденгера для стационарных состояний: (-ħ²/2m)*▼²*Ѱ+u*Ѱ=EѰ, где Ѱ=a*e^-i*(ωt-kx), E=(1/Ѱ)*i*ħ*(dѰ/dt).