2.6Выбор размеров деталей и расчеты на прочность

Расчеты на прочность проводят по двум режимам: по максимальному усилию, которое водитель может приложить к рулево­му колесу; по максимальному тормоз­ному моменту на колесах (одном или двух) на дороге с φ = 0,8…0,9. Так как методы расчетов деталей рулевого управления на усталостную проч­ность разработаны недостаточно, рас­четы носят сопоставительный харак­тер, т. е. получаемые расчетные на­пряжения сравнивают с напряжения­ми в аналогичных деталях автомоби­лей, хорошо зарекомендовавших себя в эксплуатации.

Момент на рулевом валу:

,

где F_рmax – максимальное усилие на ободе рулевого колеса прилагаемое водителем, Н.

При максимальном моменте напряжение кручения τ не превышает – 25…75 МПа. Диаметр рулевого вала найдем из формулы:

,

где W_к – момент сопротивления кручению для круглого сечения;

Допустимую длину рулевого вала найходим из формулы:

,

где G – модуль упругости второго рода, G = 7,8·10¹⁰МПа;φ – угол закручивания, φ = 5,5…7,5⁰.

В качестве материал рулевого вала можно выбрать сталь 35.

2.7Расчет деталей винтореечного рулевого механизма

Средние зубья рейки и сектора изнашиваются интенсивнее, чем крайние. Поэтому устранение зазора при среднем положении сошки может привести к заклиниванию передачи при поворотах. Чтобы не до­пустить этого, предусматривают увеличение бокового зазора в зацеп­лении при поворотах вала сошки в обе стороны от среднего положения. Достигается это путем поворота заготовки в процессе зубонарезания вокруг техноло­гической оси О₁ смещенной относительно оси О вала сошки к сектору на расстояние п(Рис. 2 .12).

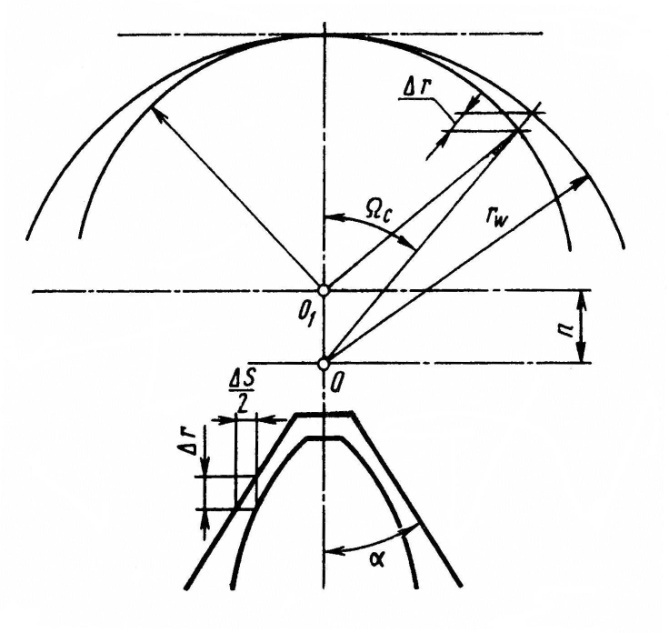
Рис. 2.12. Схема для определения радиального Δzи осевого Δs зазоров в зубчатой паре при нарезании зубьев сектора с поворотом заготовки вокруг смещенной оси O₁

Боковой зазор в передаче выбираем по графику (Рис. 2 .13).

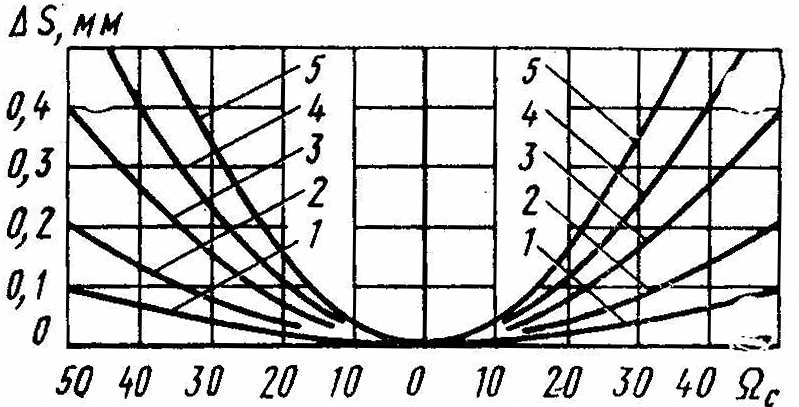
Рис. 2.13. График для выбора эксцентриситета 1—5 – соответственно при 0,25; 0,5; 1,0; 1,5 и 2,0 мм

Диаметр шариков при проектном расчете принимают в зависимости от шага винта:

,

Выбирается стандартный близкий диаметр шарикаd_ш. Выбирается материал шарика, например сталь ШХ15.

Радиус желоба r_п у винта и гайки для уменьшения трения должен быть больше радиуса шариков:

,

Внутренний и внешний диаметры канавок винта d₁и dи гайкиD₁и D (Рис. 2 .14) соответственно определяются:

,

,

,

,

где:h – глубина канавки:

,

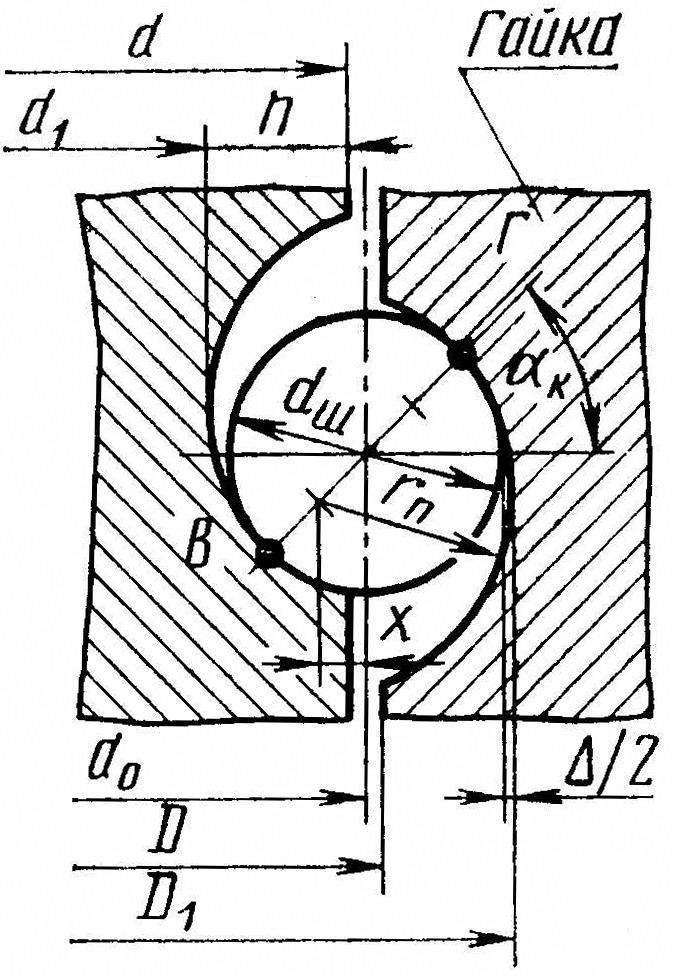
Рис. 2.14. Профили канавок винта и гайки

Смещение х центров профилей кана­вок относительно центров шариков и сред­него диаметра винтового канала d₀:

,

,

где β = 10÷15⁰ — угол подъема винтовой линии ; α_к = 45÷60⁰ — угол контакта шариков с канавками.

Полученное значение округляют с точностью до 0.5 мм.

Общее число витков в гайке:

,

Число рабочих витков в гайке n_p = 2.5.

Минимальное целое число шариков в одном витке:

,

Полученное значение z_ш округляют до ближайшего целого числа.

Зубья сектора рассчитывают на изгиб и на контактную прочность.

Модуль зацепления сектора и рейки определяют по общеизвестной методике из условий изгибной прочности:

,

где b_ω — ширина сектора, м; k_F — коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (неравномерность распределения по длине контактной линии); у_F= 3,67 — коэффициент формы зуба.

Допускаемое напряжение может быть принято [σ_и] = 850 ÷ 950 МПа.

Коэффициент нагрузки при расчете по напряжению изгиба найдем по формуле:

,

где k_Fν = 1,02 – коэффициент учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления шестерни и колеса; k_Fβ = 1,04 – коэффициент, учитывающий неравномерность распределения напря­жений у основания зубьев по ширине зубчатого венца; k_Fα = 1,06 – коэффициент, учитывающий влияние погрешностей изготовления ше­стерни и колеса на распределение нагрузки между зубьями.

Полученное значение модуля mокругляют до ближайшего стандартного значения.

Контактные напряжения:

,

где b – радиальная длина зубьев сектора, м; r_с – свободный радиус колеса, м; Е – модуль упругости второго рода, Е = 2,1∙10⁵ МПа;σ_см – напряжения смятия, σ_смmax ≤ 1500 МПа.

,

где r₀ – расчетный радиус колеса, м.

Выбирают материалы для деталей рулевого редуктора. Например для автомобилей КамАЗ материал сектора – сталь 20Х2Н4А, винта и гайки – сталь 20ХН3А, с цементацией до твердости 56...62 HRC,материал корпуса рулевого механизма – чугун КЧ 37-12.