1.4.2Малолистовые рессоры

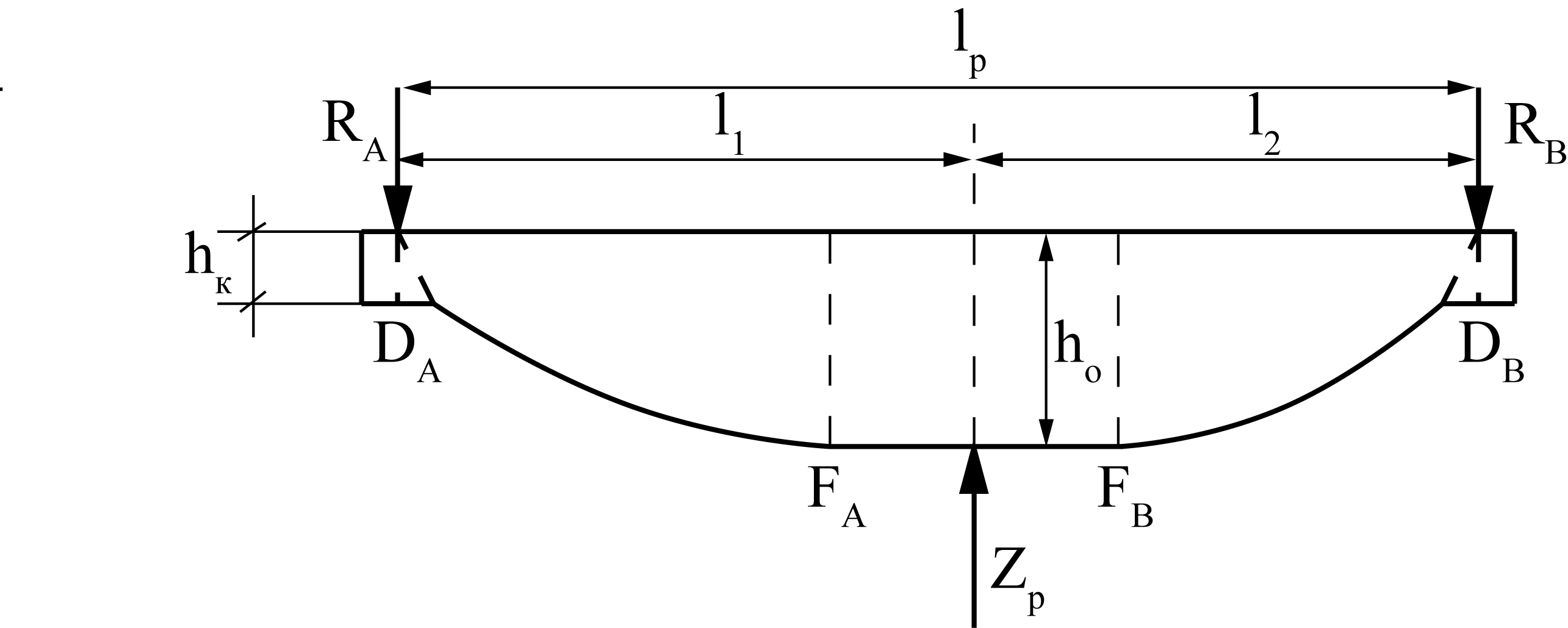
Рис. 1.4. Расчетная схема малолистовой рессоры

Рассмотрим крайний случай - однолистовая рессора.

D_AF_A, D_ВF_В – параболические участки, F_AF_В – плоские участки.

Толщина однолистовой рессоры должна вдоль рессоры изменяться по зависимости:

,

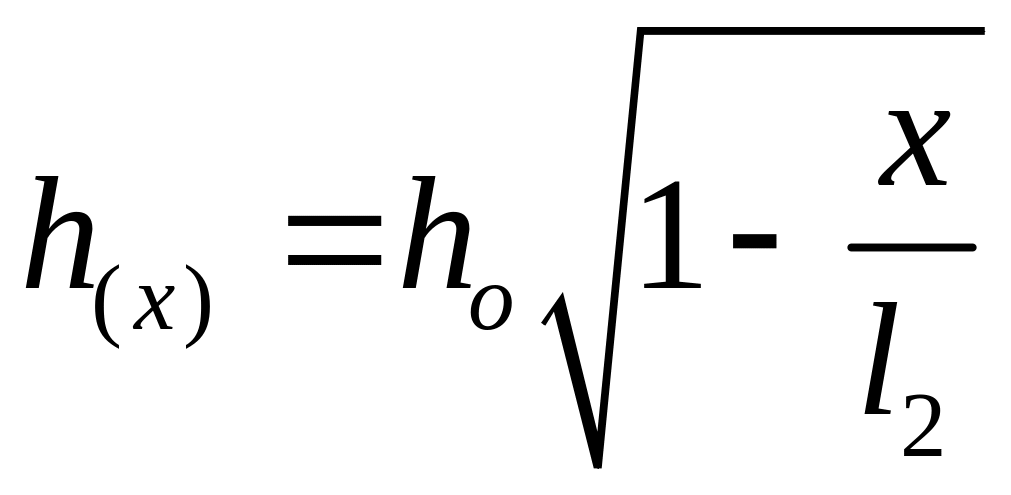где: х – расстояние от середины до рассматриваемого сечения,

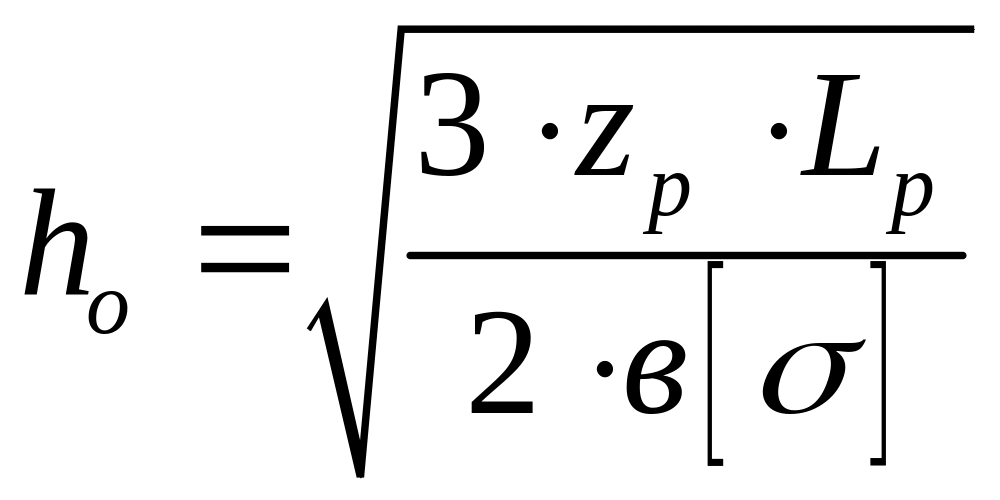, где n_x – ширина в рассматриваемом сечении.

В основу расчета положена эмпирическая зависимость:

где: n_л – число листов рессоры;

L_p – длина рессоры, мм;

σ – напряжение при статической нагрузке, МПа;

Е – модуль упругости первого рода, МПа;

f_СТ – статический прогиб рессоры, мм;

γ – коэффициент изменения прогиба по сравнению с прогибом идеальной рессоры, для которой γ = 1;

z_p – статическая нагрузка на рессору, Н;

в – ширина листа рессоры, мм.

Из зависимости (1) – вытекает определение длины рессоры:

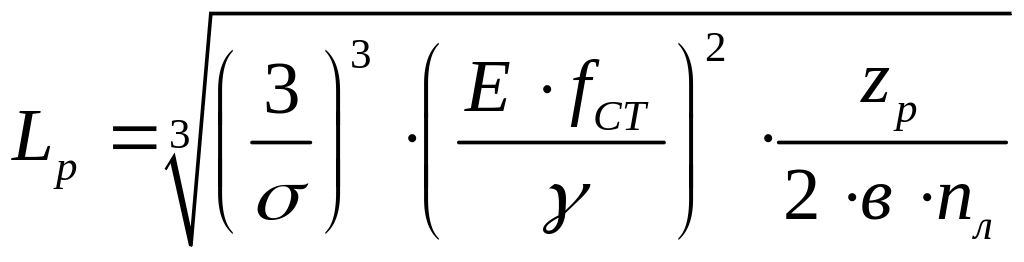
Зависимость между L_pи n_л – кубическая.

Е = 2,1·10⁵ МПа.

Допускается σ_СТ = 500…550 МПа.

Обычно однолистовая рессора получается слишком длинной, в этом случае применяют малолистовую рессору.

Малолистовая рессора представляет собой пакет однолистовых рессор, где все листы имеют одинаковую длину. Обычно применяют 2, 3 листа.

Таким образом, нагрузка распределяется между листами поровну, т.к. прогибы всех листов одинаковы, то жесткость листа будет равна:

.

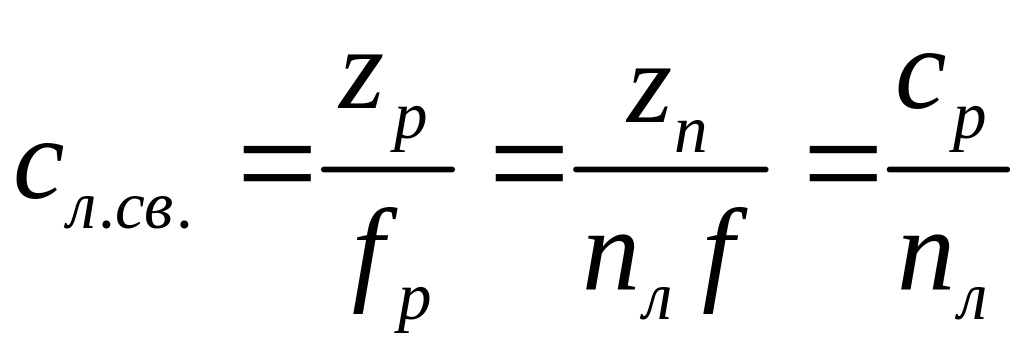Рессора после сжатия имеет жесткость несколько выше, чем в свободном состоянии.

Принимают, что в собранной рессоре эффективные длины равны:

;

, .

При этом жесткость листа рессоры с учетом заделки составляет:

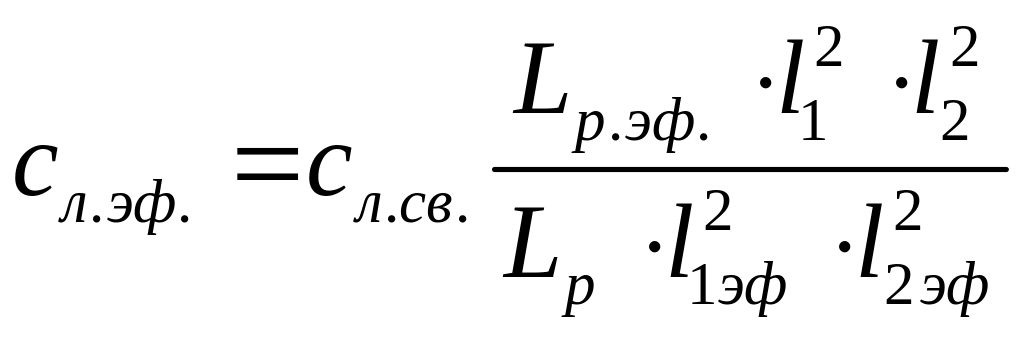
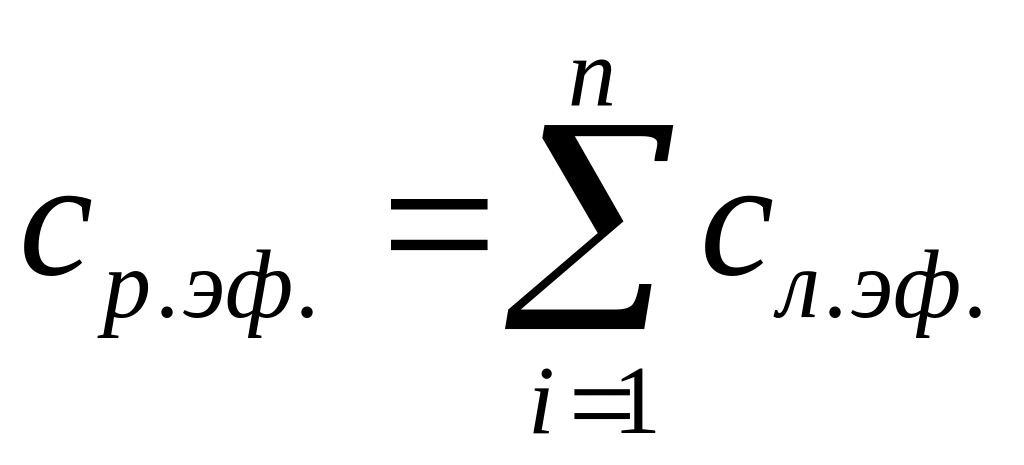
Силы могут действовать только по рычагу, остальные силы рычаг не воспринимает.

,

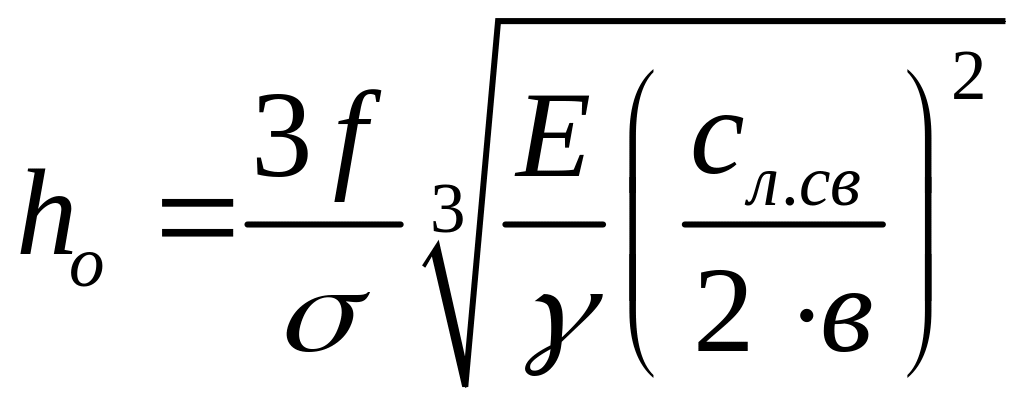
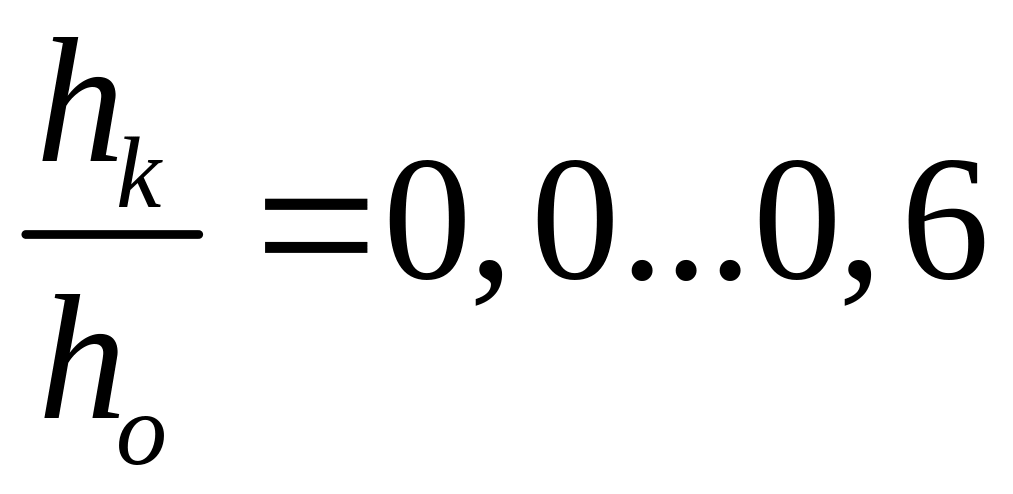F_A·F_B = 110…150 мм.

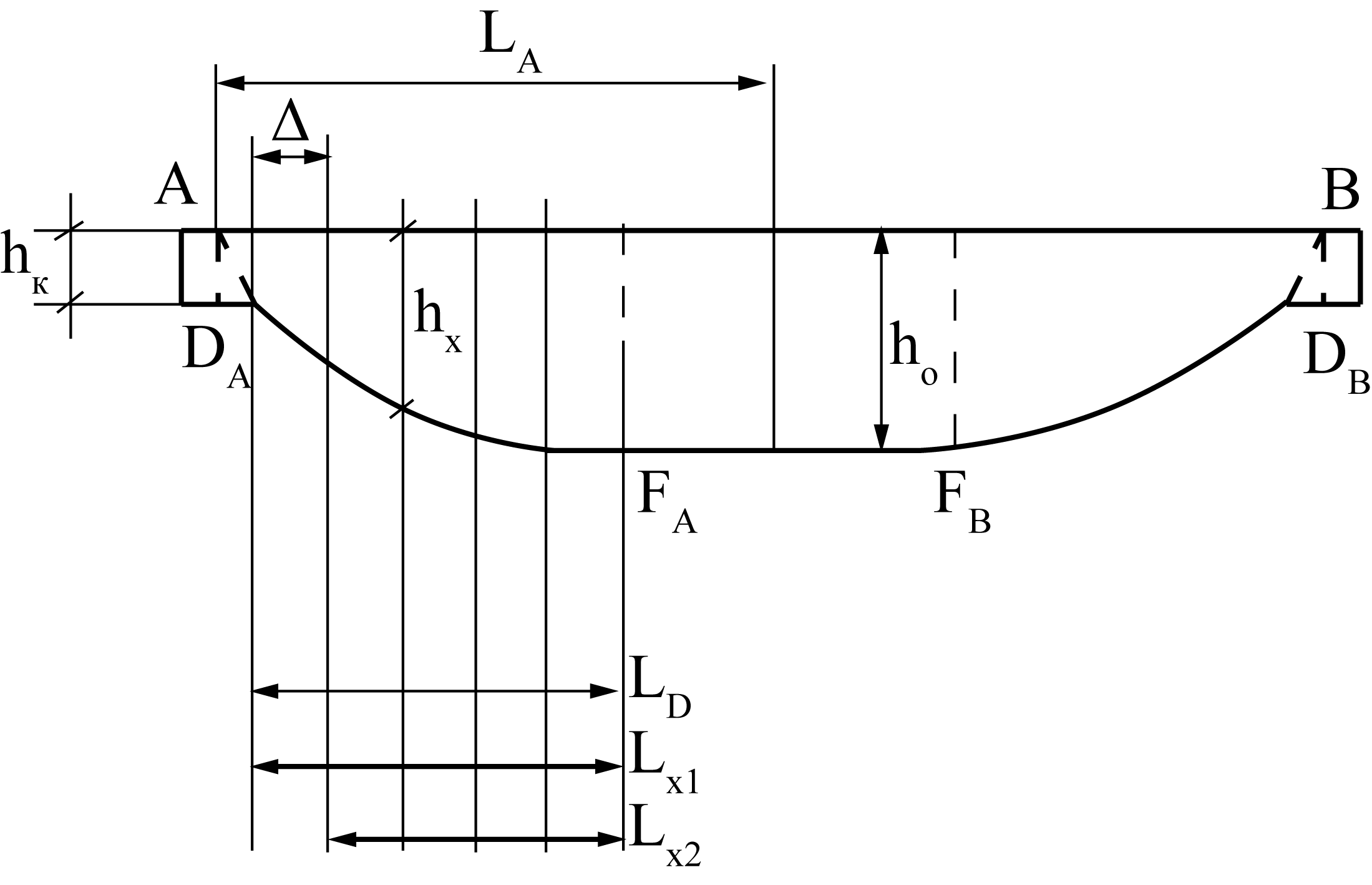
Рис. 1.5. Расчет сечения листа малолистовой рессоры

Положение точки D:

, где L_o =l₁или l₂(если симметрично, если нет, то для каждого свой расчет).

Параболический участок разбивают по длине на m–участков, длина каждого из них Δ:

.

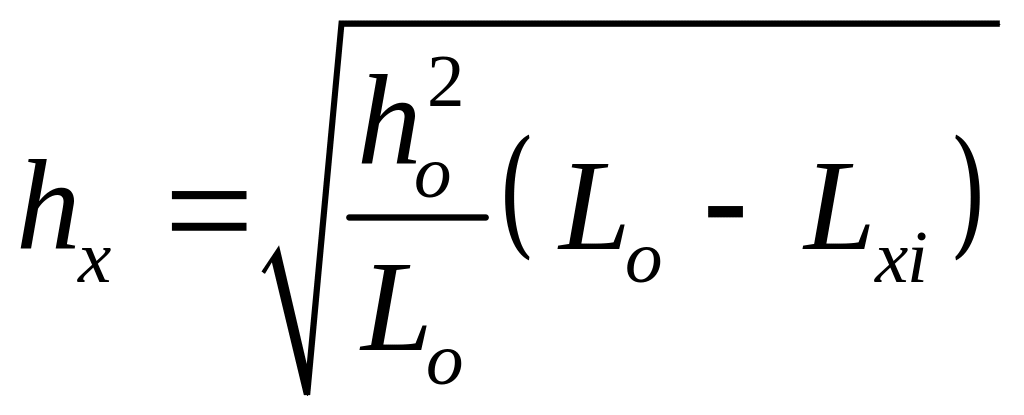R_o – радиус кривизны рессоры в свободном состоянии.

;

.

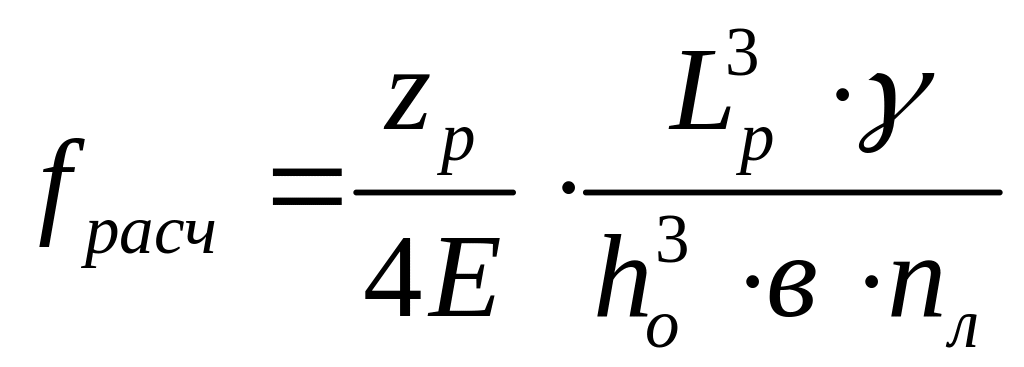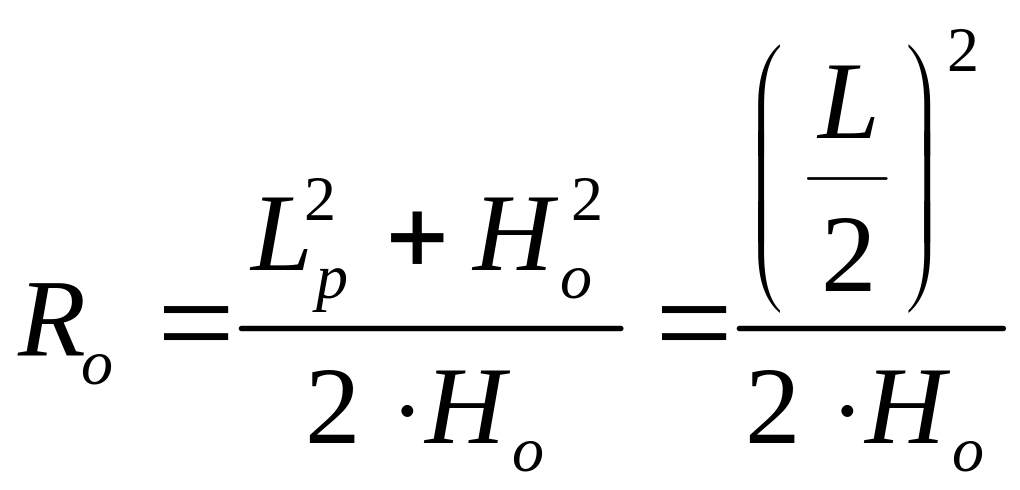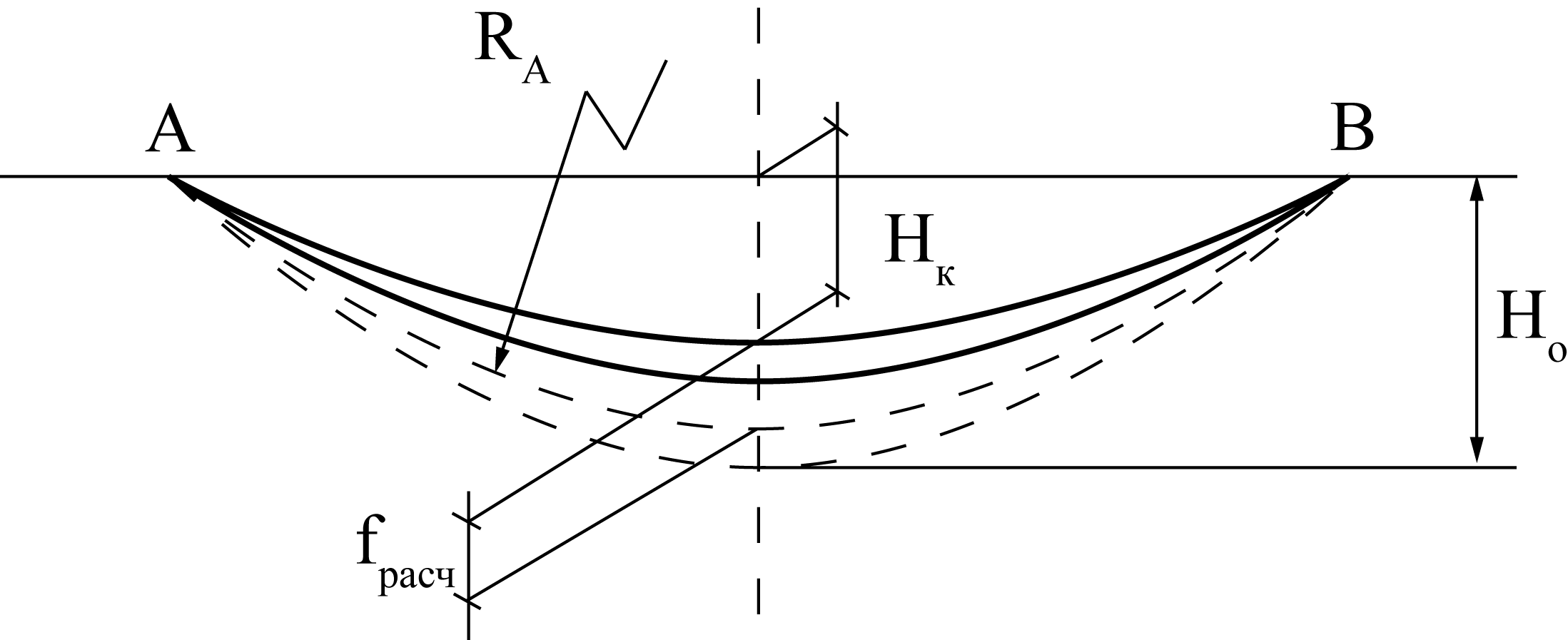
Рис. 1.6. Определение радиуса кривизны рессоры в свободном состоянии

Объем листа рессоры:

, см³,

где К_v – коэффициент использования металла:

;

;

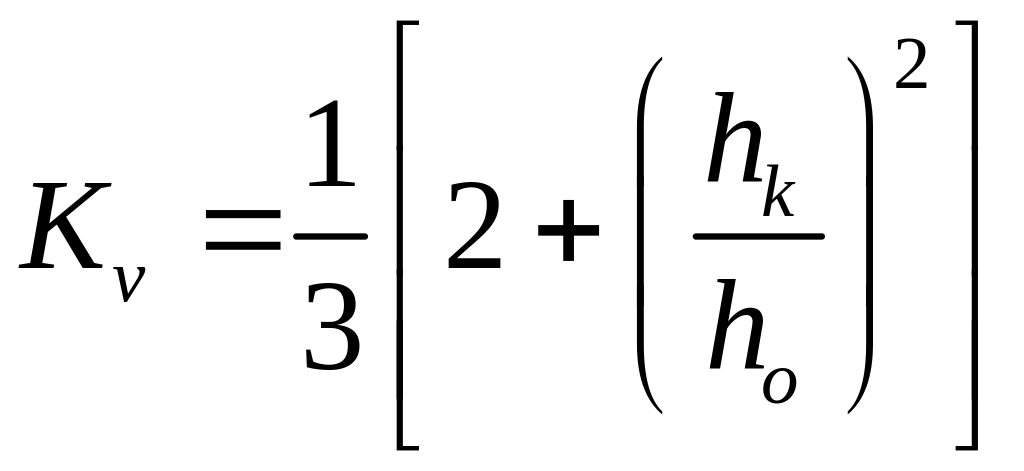ρ = 0,00785 кг/см³ – плотность пружин из стали.

Масса малолистовой рессоры получается меньше, чем многолистовой рассчитанной на такие же нагрузки.

Далее выполняют поверочные расчеты:

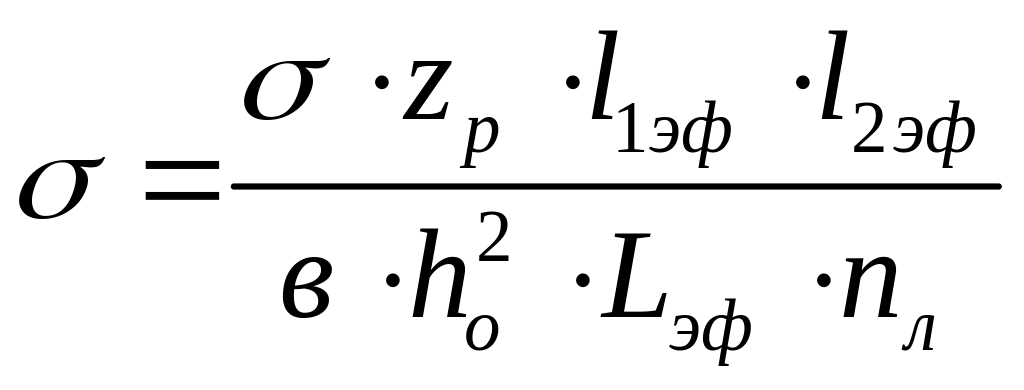
[σ_max]=1200 МПа.

Формула емкости для малолистовой рессоры:

;

.

1.4.3Расчет винтовых пружин

Энергоемкость винтовых пружин в 4 раза больше, чем у листовых рессор при одинаковом напряжении.

Материал пружин работает на кручение:

,

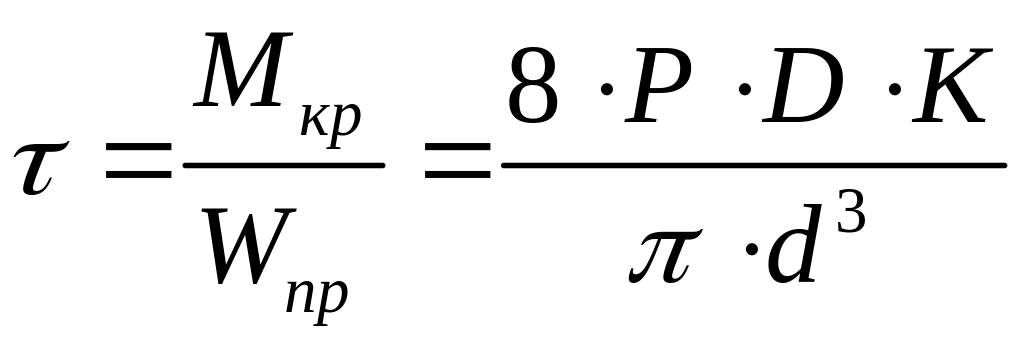где: Р – сила, действующая вдоль оси пружин;

D – диаметр витка;

d – диаметр прутка;

К – коэффициент учета увеличения напряжения на внутренней поверхности пружины.

[τ_СТ] = 350 МПа,

[τ_дин] = 550…700 МПа.

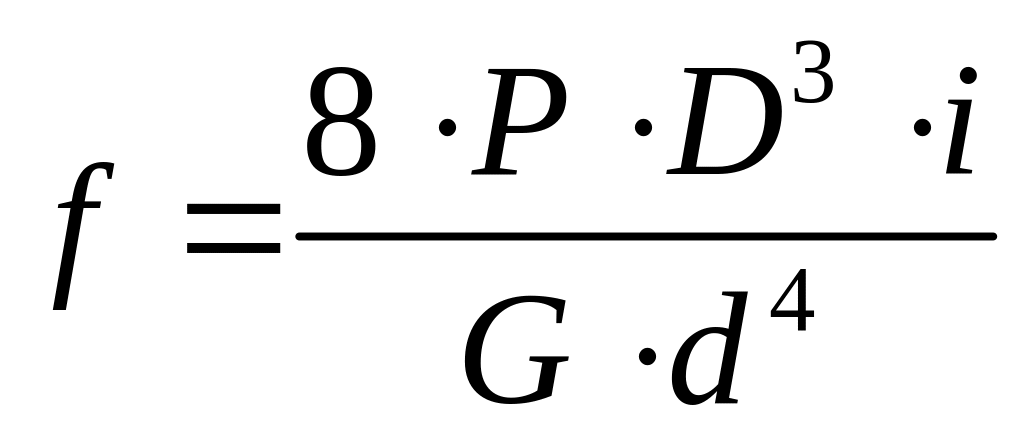, где i–количество витков (работающих).

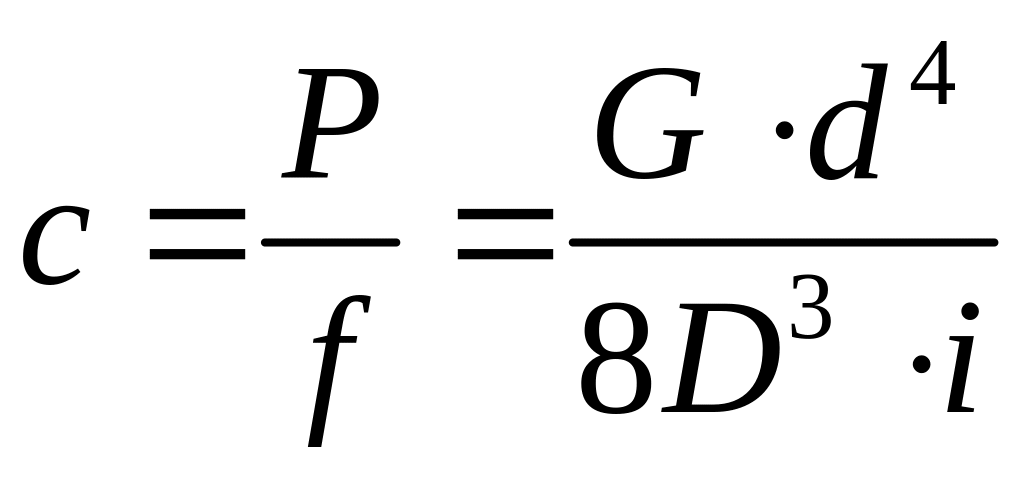, или ,

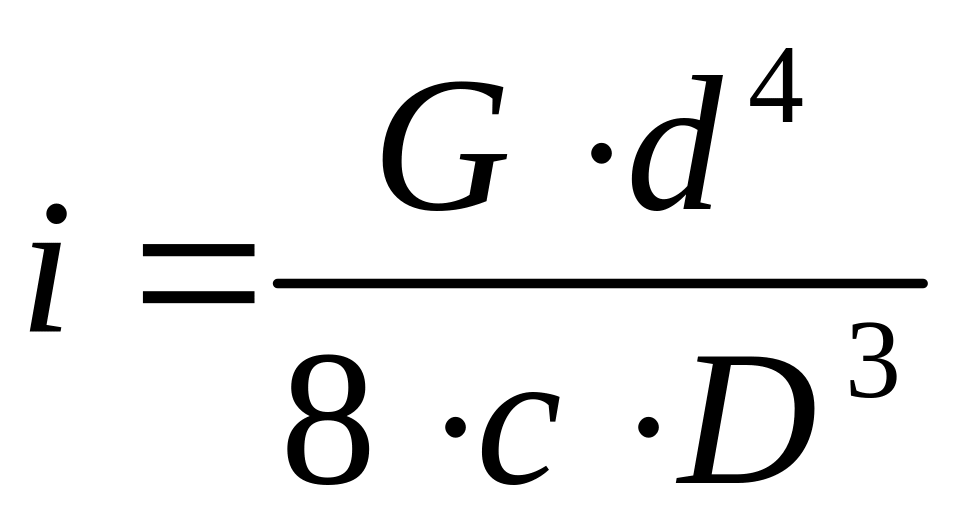, где G – модуль упругости второго рода (G = 7,8·10⁴ МПа).

1.4.4Неметаллические упругие элементы

Наиболее распространенными упругими элементами (неметаллические) – резина.

Преимущества:

• имеет нелинейную упругую характеристику;

• энергоемкость резины больше энергоемкости стали.

Недостатки:

• резина стареет со временем, ухудшает свойства со временем;

• резина чувствительна к температуре (на морозе становится жесткой).

Она мало распространена в качестве основного материала, но часто изготовляются второстепенные упругие элементы.Работает на растяжение – сжатие и на сдвиг.