22. Формирование Орг структур управления на основе кластерного анализа

Кластерный анализ — задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. 

Кластерный анализ выполняет следующие основные задачи:

• Разработка типологии или классификации.

• Исследование полезных концептуальных схем группирования объектов.

• Порождение гипотез на основе исследования данных.

• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных (примечание 1).

Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы: — Отбор выборки для кластеризации. — Определение множества переменных, по которым будут оцениваться объекты в выборке. — Вычисление значений той или иной меры сходства между объектами. — Применение метода кластерного анализа для создания групп сходных объектов. — Проверка достоверности результатов кластерного решения (примечание 1).

При построении организационной структуры важно, чтобы в одну сферу (одному руководителю) попали наиболее тесно связанные между собой задачи. Организационная структура управления обязана обеспечивать наилучшую координацию решения задач, то есть в каждой подсистеме сосредоточиваются наиболее тесно связанные между собой задачи.

Это позволяет:

• наиболее рационально распределять и перераспределять ресурсы;

• замкнуть процессы координации в рамках отдельных подсистем;

• рационально загрузить руководителей различных уровней организационных структур;

• улучшить согласование результатов решения задач, то есть минимизировать сроки и ресурсы.

Рациональной сферой деятельности считаются те, в которых сосредоточиваются наиболее тесно связанные между собой задачи.

Задача кластерного анализа состоит в том, что на основании данных содержащихся в множестве Х, разбить множество объектов I на кластеры (подмножества) таким образом, чтобы любые объекты, принадлежащие одному и тому же кластеру были сходны в то время как объекты, принадлежащие разным кластерам были различны.

Например рассмотрим, I={I₁, I₂, … I_n}, как множество кластеров {I₁}, {I₂}, …{I_n}. Выберем два из них {I_i} и {I_j}, которые по какому-то признаку наиболее близки друг к другу и объединим их в один кластер {I_i, I_j}. Новое множество будет состоять из (n-1) объектов. Повторяя процесс, мы получим последовательные множества кластеров, состоящие из (n-2), (n-3) и т.д. кластеров.

Использование аппарата кластерного анализа сводиться к последовательному объединению элементов в однородные сферы деятельности (трудоемкость объединяемых в один кластер работ не может быть более 1840 часов в год).

Этапы проведения последовательной кластеризации: (можн не писать)

1. Анализ организационной структуры и функционального разделения труда.

2. Выделение основных задач выполняемых в рамках организационной структуры управления (элементы деятельности).

3. Построение операционной матрицы, характеризующей каждый элемент деятельности.

Признаки Элементы	Вход	Процессор	Выход	…	Трудоемкость, час
a b n	10101… 01010…

Выделение характеристик для элементов деятельности – творчество эксперта. Задача состоит в том, чтобы подобрать характеристики наиболее полно описывающие элементы деятельности.

4. Заполнение операционной матрицы. Каждая строка описывается вектором оценок, характеристических признаков. Если признак присутствует, то в матрице ставится «1», если отсутствует, то «0».

5. Определение расстояния между векторами – характеристическими признаками.

R_ab= |x_a-x_b|, где

R_ab – расстояние между вектором а и вектором b,

x_a, x_b – характеристики векторов а и b соответственно.

Сложив их, получаем расстояние между вектором a и вектором b.

6. Построение матрицы расстояний размерности n n.

	1	2	.	.	.	n
1	x
2		x
. расстояние			x
.				x
.					x
n						x

7. В полученной матрице находится минимальный элемент, координаты которого соответствуют векторам, объединяемым в один кластер, если выполняется ограничение. Если ограничение не выполняется, выбранному минимальному элементу присваивается значение бесконечности.

8. Объединение векторов с пересчетом матрицы расстояний. Так как мы объединяем два вектора в один, то размер новой матрицы будет (n-1) (n-1).

{d_i}

{d_к}

{d_j}

Расстояние в новой матрице определяется по формуле:

R_ijk= , где

n_i – количество элементов в векторе {d_i}

n_j – количество элементов в векторе {d_j}

n_k – количество элементов, в новом векторе {d_k}

R_ij – разрешающий минимальный элемент

R_ijk – расстояние между векторами d_i , d_j и d_k.

R_ik – расстояние между векторами d_i и d_k.

R_jk – расстояние между векторами d_j и d_k.

Объединение векторов производится до тех пор пока соблюдаются ограничения. Если не возможно произвести объединение не нарушив ограничения, кластеризация заканчивается.

9. Путем кластеризации элементов деятельности формируется состав сфер для первого уровня. Затем используя полученные результаты можно формировать сферы последующих уровней. Для решения этой задачи необходимо найти положение в признаковом пространстве уже сформированных сфер. В качестве характеристического признака используется характеристический вектор элемента репрезентанта, то есть элемента, характеристика которого наиболее полно отражает особенности сферы в целом. При этом возможны следующие варианты.

• Если число элементов в сфере один, то его характеристики наиболее сильно отличаются от других сфер, поэтому он является репрезентантом.

• Если элементов в сфере больше двух, то для каждого элемента d_i в данной сфере рассчитывается сумма расстояний его до остальных элементов этой сферы 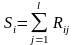, где l – число элементов сферы. Репрезентантом будет элемент имеющий S_i – минимальное.

• Если число элементов в сфере равно двум для каждого элемента этой пары рассчитывается сумма его расстояний до всех остальных элементов репрезентантов, выбранных на предыдущих этапах. Репрезентантом будет элемент, имеющий максимальную сумму расстояний.