11.3. Ошибки выборки.

На основании зарегистрированных в соответствии с программой статистического наблюдения значений признака единиц выборочной совокупности рассчитываются обобщающие выборочные характеристики:

• Выборочная средняя

• Выборочная для единиц, обладающих каким-либо интересующим исследователей признаком, в общей их совокупности

Разность между показателями выборочной и генеральной совокупностей называется ошибкой выборки.

Ошибки выборки как и ошибки любого другого вида статистического наблюдения подразделяются на ошибки регистрации и ошибки репрезентативности.

Основной задачей выборочного метода является изучение и измерение случайных ошибок репрезентативности.

Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяется средняя из возможных ошибок.

Средняя ошибка выборки для величины рассчитывается по формуле:

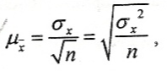
Средняя ошибка выборки для доли единиц определенного признака рассчитывается:

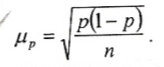
Утверждать, что генеральные средние значения признака или генеральная доля не выйдет за границы средней ошибки выборки можно лишь с определенной степенью вероятности. Поэтому для характеристики ошибки выборки, кроме средней ошибки, рассчитывают предельную среднюю ошибку выборки, которая зависит от гарантирующего ее уровня вероятности. Уровень вероятности (Р) определяет величина нормированного отношения (t), и наоборот.

Наиболее часто используемые сочетания Р и t, в таблице «Значения нормированного отклонения t при соответствующих значениях уровней вероятности Р».

Нормальное отклонение (t) – коэффициент доверия, зависящий от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t-кратную среднюю ошибку. Этот коэффициент показывает сколько средних ошибок содержится в предельной ошибке. Например, если t=1, то с вероятностью 0,683 можно утверждать, что разность между оборотными и генеральными показателями не превысит одной средней ошибки.

После исчисления предельных ошибок выборки находят доверительные интервалы для генеральных показателей. Вероятность, которая принимается при расчете ошибки выборочной характеристики называется доверительной.

Доверительный уровень вероятности 0,95 означает, что в 5 случаях из 100 ошибка может выйти за установленные границы; вероятности 0,954 – 46 случаях из 1000, а при 0,999 – в 1 случае из 1000.

Для генеральной средней и генеральной доли наиболее вероятные границы, в которых они будут находиться с учетом предельной ошибки репрезентативности, представлены формулами:

При стратифицированном отборе в выборку обязательно попадают представители всех групп обычно в тех же пропорциях, что и в генеральную совокупность. Поэтому ошибка выборки в данном случае зависит главным образом от средних из внутригруппировачных дисперсий. Исходя из правила сложения дисперсий можно сделать вывод, что ошибка выборки для стратифицированного отбора всегда будет меньше, чем для собственно случайного.

При серийном отборе мерой колеблемости будет межгрупповая дисперсия.