10.5. Индексы с постоянной и переменной базой сравнения.
При изучении динамики показателей хозяйственной деятельности предприятия и других явлений возникает необходимость определения индекса за более, чем 2 периода. В таких случаях индексы могут рассчитываться как на основе постоянной, так и переменной баз сравнения.
Цепные и базисные (вопрос 1).
Особенности расчета индивидуальных и общих индексов количественных и качественных показателей с постоянной и переменной базой сравнения рассматривают на примере базисных и цепных индексов физического объема, цен и товарооборота:
Для индивидуальных индексов цен, физического объема и индексов стоимости продукции справедливо правило состоящее из двух частей:
Произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода, т.е. выполняется равенство:
Отношение базисного индекса i-того периода к базисному индексу предшествующего i-1 периода дает цепной индекс i-того периода:
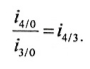
Это правило позволяет применять, так называемый, цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным индексам и наоборот.
Применения цепного метода исчисления индексов для общих индексов возможно только для агрегатных индексов физического объема с постоянными (фиксированными на уровне одного и того же периода) соизмерителями.
Так,
базисный индекс физического объема
отчетного периода может быть получен
перемножением соответствующих цепных
индексов, если соизмеритель принимается
на уровне одного и того же периода (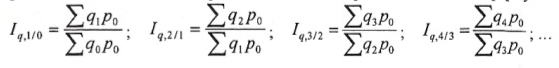
),
т.е. выполняется неравенство:
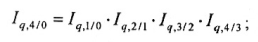
Два
смежных базисных индекса физического
объема с постоянным соизмерителем
Iq,i/0
и
Iq,
i-1/0
позволяют
получить цепной индекс i-того
периода Iq,
i/i-1
(
),
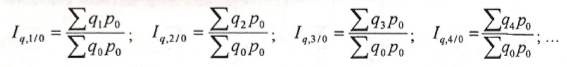т.е. выполняется равенство:
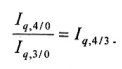
Применение цепного метода для агрегатных индексов физического объема оказалось возможным благодаря использованию в качестве соизмерителя фиксированных (соизмеримых, сопоставимых) цен.
Агрегатные индексы качественных показателей всегда являются индексами с переменными весами, т.к. количество продукции каждый раз принимается на уровне отчетного периода. Поэтому цепной метод расчета индексов не применим к агрегатным индексам качественных показателей.
10.6. Индексы средних величин.
При изучении процессов происходящих в народном хозяйстве вместе с абсолютными величинами широко используются и средние величины. При оценке динамики экономического явления средний уровень рассчитывается, как правило, для качественных признаков и определяется он как средняя арифметическая взвешенная.
На среднюю величину влияют, с одной стороны, значения признака, который усредняют, с другой, - частоты вариант. Поэтому при анализе изменения средних величин качественных показателей важно определить в какой мере оно обусловлено изменением собственно индексируемой величины, а в какой – структурными сдвигами в распределении единиц совокупности.
Структурные сдвиги в экономике – важнейший фактор развития производственных сил общества. Так, например, средняя выработка на одного работающего в какой-либо отрасли промышленности может расти не только благодаря тому, что этот показатель соответственно изменился на отдельных предприятиях, а и потому, что в общей совокупности предприятия этой отрасли увеличивают удельный вес предприятий с более высоким уровнем производительного труда на одного работающего. Такие структурные сдвиги влияют на динамику явления, более того они часто приводят к, так называемым, «статистическим парадоксам», когда изменение средних величин выходит далеко за пределы изменения исследуемых индивидуальных значений показателей.
Для характеристики изменения средних величин рассчитываются индексы переменного состава, постоянного, структурных сдвигов, формирования систем взаимосвязанных индексов, представлены для цены формулой:
Смотреть вопрос 1.