5.2. Мода и медиана

Для характеристики центральной тенденции (положения центра) рр, кроме средней арифметической, применяются структурные средние, используемые для изучения внутреннего строения рр. В отличие от средней арифметической, рассчитываемой на основе всех вариант, мода и медиана характеризуют значения признака у единиц совокупности, занимающих определенное положение в вариационном рр.

Медиана – значение признака единиц совокупности, стоящей в середине упорядоченного ряда и делящей совокупность на две, равные по численности части. В итоге у одной половины единиц совокупности значения признака не превышают медианного уровня, а у другой – не меньше его. Медиану (Ме) используют как наиболее надежный показатель типичного значения признака единиц неоднородной совокупности. Т.к. она нечувствительна к крайним значениям признака, кот. могут значительно отличаться от основного массива его значений. При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при 10 значениях признака – среднюю из 5 и 6-го значений в ранжированном ряду. В дискретном вариационном ряду медианой следует считать значение признака в той группе единиц совокупности, в которой накопленная частота превышает половину численности совокупности. В интервальном вариационном ряду для расчета медианы применяется формула 5.3.

При нечетном числе единиц совокупности номер медианы равен не

Мода – варианта, кот. в изучаемом рр встречается чаще всего. Если два или несколько значений признака встречаются равное кол-во раз, вариационный ряд считается бимодальным или мультимодальным. Это говорит о неоднородности совокупности.

В дискретном вариационном ряду модой является варианта, имеющая наибольшую частоту.

В интервальном вариационном ряду модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи кот.плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения вариирующего признака, достигает максимума. Это условное значение считается точечной модой. В интервальном вариационном ряду для нахождения моды используется формула 5.4.

Мода широко применяется в стат.практике при изучении покупательского спроса, регистрации цен. При выборе конкретного показателя центра распределения исходят из таких рекомендаций:

1) для устойчивых соц.-эк.процессов (однородных совокупностей) в качестве показателя центра используют среднюю арифметическую величину. Такие процессы характеризуются симметричным распределением, в кот.

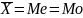
2) для неустойчивых процессов положение центра распределения характеризуется с помощью моды и медианы.

Для ассиметричных процессов предпочтительной характеристикой центра распределения явл медиана, поскольку она занимает положение м/у средней арифметической величиной и модой.

5.3. Показатели вариации

При определении общего характера распределения важнейшей задачей явл оценка степени его однородности. Однородность стат совокупностей характеризуется велчиной вариации значений признака.

Вариация – несовпадение уровней значений признаков у единиц совокупности миеет объективный характер и помогает познать сущность изучаемого явления. Для измерения вариаций статистике применяют несколько способов. Наиболее простым явл расчет показателя размаха вариации как разницы м/у макс и миним наблюдаемыми значениями признака по формуле:

Размах вариации улавливает только крайние отклонения значений признака, но не отражает отклонений от средней величины всех вариант в ряду. Чем больше размах вариации, тем менее однородна исследуемая совокупность. Точнее характеризуют вариацию признака показатели, основанные на учете колеблемости (отклонений) всех значений признака от среднего уровня признака. От размера и распределения отклонений зависят типичность и надежность средних характеристик. Средние отклонения значений признаков каждой единицы совокупности от среднего значения признака в целом, отражают показатели вариации. Показатели вариации используются для оценки степени однородности исследуемой совокупности по вариирующему признаку и типичности средней величины.

Простейший показатель такого типа – среднее линейное отклонение, представляющее собой среднее арифметическое значение абсолютных отклонений признака от его среднего уровня. Среднее линейное отклонение рассчитывается по формулам 5.6 и 5.7.:

- по не сгруппированным данным

- по сгруппированным данным:

Чем меньше 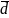, тем более однородны значения признака изучаемого явления. Основной недостаток этого показателя заключается в том, что при его расчетах пренебрегают знаками, следовательно, конечный результат получается со значительной погрешностью.

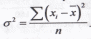Для того, чтобы расчет был более точным определяют средний квадрат отклонений (дисперсию), представляющую собой средний квадрат отклонений значений признака от его среднего уровня.:

- по не сгруппированным данным

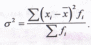
- по сгруппированным данным

Среднее квадратическое отклонение рассчитывается по формуле

явл абсолютной мерой вариации и зависит не только от степени вариации признака, но и от абсолютных уровней вариант и средней, что не позволяет непосредственно сравнивать средние квадратические отклонения вариационных рядов с разными уровнями, выражается в тех именованных числах, в кот выражены варианта и средняя величина. Для сравнительной характеристики вариационных рядов с разными уровнями по степени надежности их средние величины и однородности исследуемых совокупностей рассчитывается относительная мера вариации – коэф вариации:

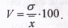
Чем больше значение коэф-а вариации, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна (типична) средняя величина. Дисперсия имеет ряд математ св-в, упрощающих технику ее расчета

Математические свойства дисперсии, упрощающие технику ее расчета:

1) если от всех вариант ряда распределения отнять какое-то постоянное число А, то диспер­сия от этого не изменится.

2) если все значения вариант разделить на какое-то постоянное число h, то дисперсия уменьшится от этого в h раз, а среднее квадратическое отклонение — в h раз.

Эти свойства положены в основу расчета дисперсии способом моментов. Способ моментов применим в том случае, если задан интервальный ряд с равными интервалами.

Дисперсия методом моментов:

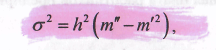
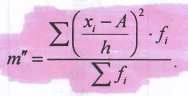
Для расчета дисперсии в любых рядах рр применяется др. упрощенный метод расчета дисперсии – способ разности. Способ разности применяется для расчета дисперсии в любых рядах распределения (дис­кретных и интервальных с равными и неравными интервалами).