5.1. Понятие рядов распределения

Среди простых группировок особо выделяют ряды распределения.

Ряд распределения в статистике – упорядоченное распределение единиц совокупности на группы по какому-либо признаку. В зависимости от признака, положенного в основание ряда распределения различают атрибутивные и вариационные ряды распределения (рр). РР, построенный по описательному признаку назыв. атрибутивными рядами. РР, построенный по количественному признаку, назыв. вариационными рядами. В вариационном ряду различают два элемента (варианты и частоты). Варианты (х) – отдельные значения группировочного признака, которые он принимает в вариационном ряду, т.е. конкретные числовые значения признака единиц совокупности. Числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения назыв. частотами (f). Частоты могут быть заданы и как относительные величины структуры (в % или долях единицы). В этом случае их назыв. частостями. Сумма всех частот определяет численность всей совокупности, т.е. ее объем (N).

По своей конструкции вариационный ряд состоит из двух столбцов:

- один столбец – значение вариирующего признака

- другой – частоты или частости.

Схематичный пример вариационного ряда приведен в табл.5.2.

Вариационные ряды по способу построения могут быть двух видов:

- дискретные

- интервальные

Дискретные вариационные ряды характеризуются тем, что варианты в них имеют значения отдельных целых чисел. Если число вариант велико или признак имеет непрерывную вариацию, то объединение отдельных наблюдений в группы возможно, лишь на базе интервала.

Интервальные вариационные ряды характеризуются тем, что значения вариант в них заданы в виде интервалов. Если вариационный ряд имеет группы с неравными интервалами, то частоты в отдельных интервалах непосредственно не сопоставимы, т.к. зависят от ширины интервала.

Для того, чтобы частоты можно было бы сравнить исчисляют плотность распределения – частоту (т.е. число единиц совокупности), рассчитанную на единицу ширины интервала.

Для изображения вариационных рядов применяют линейные и плоскостные диаграммы, построенные в прямоугольной системе координат. При дискретной вариации признака, графиком вариационного ряда служит полигон распределения. Графическим изображением интервальных вариационных рядов служит гистограмма. При неравных интервалах гистограмма строится только по плотности распределения. При построении графиков рр по оси абсцисс приводятся варианты, а по оси ординат – соответствующие им частоты (частости). Для иллюстрации рр используются также кумуляты и огивы. Для их построения на оси абсцисс отмечаются значения дискретного признака (или концы интервалов), а на оси ординат – нарастающие итоги частот (кумулята) или частостей (огива), соответствующим этим значениям признака.

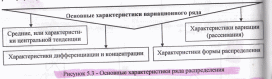
Вариационные ряды дают возможность установить характер распределения единиц совокупности по тому, или иному кол-венному признаку с помощью расчета 4-х видов характеристик (групп показателей), указанных на рис.5.3.

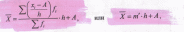
К показателям, характеризующим центральную тенденцию рр, относят среднюю арифметическую взвешенную величину значений группировочного признака и соответствующие структурные средние. Средняя арифметическая по данным интервального вариационного ряда рассчитывается методом моментов по формуле:

Анализ показателей, характеризующих тенденцию рр, степень вариации, дифференциации и концентрации значений вариирующего признака, а также форму их распределения позволяет дать комплексную оценку характера распределения единиц совокупности.