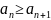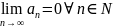- •Свойства интегралов по фигуре от скалярных функций.
- •Применение интегралов по фигуре от скалярной функции в геометрии.
- •Криволинейный интеграл 1 рода. Определение и простейшие свойства.
- •Вычисление криволинейного интеграла 1-го рода по кривой на плоскости в зависимости от способа задания кривой.
- •Вычисление криволинейного интеграла 1-го рода по кривой в пространстве.
- •Приложения криволинейного интеграла 1-го рода в механике и геометрии.
- •Поверхностный интеграл 1-го рода. Определение и простейшие свойства этого интеграла.
- •Вычисление поверхностного интеграла 1-го рода сведеением к двойному интегралу.
- •Приложения поверхностного интеграла 1-го рода в механике.
- •Интеграл по ориентированной фигуре от векторной функции. Теорема существования. Простейшие свойства.
- •Независимость криволинейного интеграла 2-го рода от пути интегрирования (случай плоской кривой). Нахождение ф-ии по ее полному дифференциалу.
- •Двойной интеграл. Определение, геометрический сымсл двойного интеграла.
- •Свойства двойного интеграла.
- •Вычисление двойного интеграла в декартовых координатах.
- •Приложения двойного интеграла в механике.
- •Тройной интеграл. Определение и простейшие свойства тройного интеграла.
- •В ычисление тройного интеграла в декартовых координатах. Приложения тройного интеграла в геометрии.
- •Тройной интеграл в сферических координатах.
- •Тройной интеграл в цилиндрических координатах.
- •Приложения тройного интеграла в механике.
- •Скалярное поле. Поверхности и линии уровня скалярного поля.
- •Производная по направлению. Градиент.
- •Векторное поле. Векторные линии и их уравнения.
- •Поток, дивергенция векторного поля. Теорема Остроградского-Гаусса.
- •Циркуляция и ротор векторного поля. Теорема Стокса.
- •Потенциальное векторное поле. Нахождение потенциала.
- •Соленоидальное и гармоническое векторные поля и их простейшие свойства.
- •Числовые ряды. Сходимость и сумма рядов. Простейшие свойства рядов. Необходимое условие сходимости числового ряда.
- •Знакопеременные ряды. Достаточный признак сходимости. Абсолютная и условная сходимости.
- •Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
- •Ряды с комплекными членами.
- •Функциональные ряды. Область сходимости. Понятие ранвомерной сходимости. Признак Вейерштрасса.
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус сходимости. Интервал сходимости.
Знакопеременные ряды. Достаточный признак сходимости. Абсолютная и условная сходимости.
Ряды, содержащие как положит так и отриц члены.
Теорема.
Пусть дан ряд
,
рассм
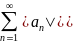 - знакоположит ряд.
- знакоположит ряд.
Теорема Коши. Если сходится ряд, состоящий из модулей , то сходится и знакопеременный ряд .
Определение. Если сходится ряд из модулей, то знакопеременный ряд абсолютно сходящийся, а если сходится, а ряд расходится, то ряд условно сходящийся.
Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
Это ряды, члены которых поочередно меняют знак.
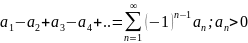
Теорема Лейбница. Если все члены знакочеред ряда удовлетв условиям:
То
ряд
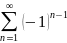 сходится и его сумма
сходится и его сумма
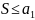 .
Такие ряды – ряды Лейбница.
.
Такие ряды – ряды Лейбница.
Следствие.
Остаток
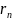 ряда
Лейбница
ряда
Лейбница
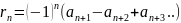 удовл нерав-ву
удовл нерав-ву
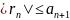
Ряды с комплекными членами.
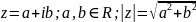

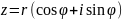
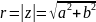
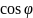
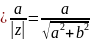
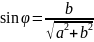

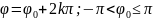
Числовой
ряд (1)
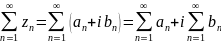 ;
;
 ;
;
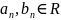 -
ряды с комплексными членами.
-
ряды с комплексными членами.
- действит часть ряда - мнимая часть ряда.
 ;
– если сущ, то ряд сходится.
;
– если сущ, то ряд сходится.
Сходится тогда и только тогда, когда сходятся ряды из действит и мнимой частей, при этом
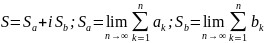
Теорема.
Если сходится ряд
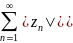 ,
то сходится и ряд
,
то сходится и ряд
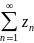
Ряд (1) называется абсолютно сходящимся, если сходится ряд из модулей .
Сходящийся ряд (1), которому соотв расходящийся ряд из модулей называется условно сходящимся.
Ряд
(1) сходится абсолютно, когда сходятся
и
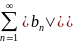 .
Если ряд (1) сходится абсолютно, то он
сходится.
.
Если ряд (1) сходится абсолютно, то он
сходится.
Если
сходится, то
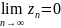 .
Если
.
Если
 ,
то
расходится.
,
то
расходится.
Функциональные ряды. Область сходимости. Понятие ранвомерной сходимости. Признак Вейерштрасса.
Рассм
послед-ть
 (1)
(1)
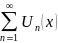 – функциональный ряд, заданный на
множестве X.
– функциональный ряд, заданный на
множестве X.
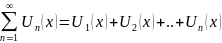
 – сходится,
то
– сходится,
то
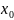 – точка сходимости функц ряда (1).
Множество всех точек сходимости –
область сходимости ряда.
– точка сходимости функц ряда (1).
Множество всех точек сходимости –
область сходимости ряда.
D
– область сходимости функц ряда (1).
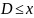
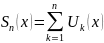 ;
;
 ;
;

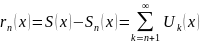
Если
(1) сходится, то
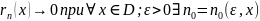
 ряд
(1) сходится с точке х.
ряд
(1) сходится с точке х.
Функц
ряд (1) равномерно сходится в D
в ф-ии S(x),
если для любого
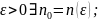
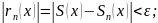
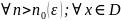 .
Поточечная сходимость – неравномерная.
.
Поточечная сходимость – неравномерная.
Признак
Вейерштрасса. Если члены функц ряда
удовл условию
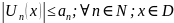 и ряд
сходится, то ряд (1)
сходится равномерно в области D.
и ряд
сходится, то ряд (1)
сходится равномерно в области D.
Замечание 1. Признак Вейерштрасса – достаточное условие равномерной сходимости.
Замечание 2. Мажорируемость ряда явл достаточным условием его равномерной сходимости, а также и абсолютной сходимости в этой же облачти D.
Свойства равномерно сходящихся функциональных рядов.
Теорема о непрерыности суммы функционального ряда. Если на множестве D функц ряд с непрерывными членами сходится равномерно, то его сумма S(x) непрерывна на области D.
Теорема о почленном интегрировании функционального ряда. Если функц ряд с непрерывными членами сходится к ф-ии S(x) на отрезке
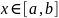 ,
то его можно почленно интегрировать
на
,
то его можно почленно интегрировать
на
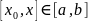 .
Справедливо равенство:
.
Справедливо равенство:
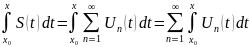 .
При этом ряд
.
При этом ряд
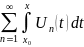 сходится равномерно на
.
сходится равномерно на
.Теорема о почленном дифференцировании функционального ряда. Дан функц ряд ,
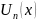 непрерывно дифференцируема на
.
Если ряд (1) сходится к ф-ии S(x),
а ряд
непрерывно дифференцируема на
.
Если ряд (1) сходится к ф-ии S(x),
а ряд
 сходится равномерно на
,
то исходный ряд (1) сходится равномерно
на
,
а его сумма S(x)
непрерывно дифференцируема на
.
сходится равномерно на
,
то исходный ряд (1) сходится равномерно
на
,
а его сумма S(x)
непрерывно дифференцируема на
.