26. Производная по направлению. Градиент.

Напишем среднюю скорость изменения потенциала в напрвлении вектора 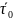в точке

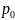
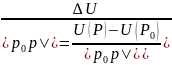
Если существует 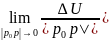, то он называется скоростью изменения в точке в направлении .

Производная ф-ии в по направлению вектора называется пределом относительного приращения ф-ии 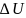к величине 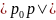при .

Если перемещение в направлении происходит по линии l, то производная по направлению: ;

;

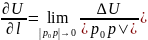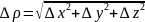
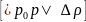
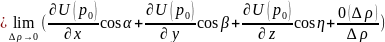
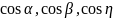– направляющие косинусы вектора .

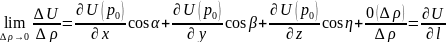– производная по направлению.

Градиент скалярного поля.Градиентом скалярного поля в точке 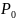(в случае, когда 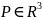), называется вектор, проекциями которого на оси координат являются частные производные от ф-ии по соотв переменным.

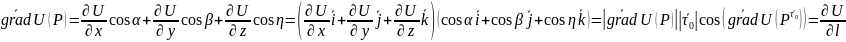
Направление градиента явл направлением ближайшего изменения потенциала скалярного поля. Градиент направлен по нормали к пов-ти уровня в этой точке.

26. Векторное поле. Векторные линии и их уравнения.

Стационарное вект поле – пространство либо какая-либо область V, т. . ( ).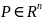

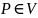– задана векторная ф-я, где 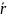– радиус-вектор точки Р.

Если 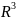, то: ;

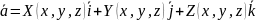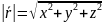
основные характеристики: векторные, силовые линии; поток, дивергенция, ротор, циркуляция.

Векторная линия векторного поля – линия, в каждой точке Р которой вектор 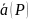расположен по касательной к этой линии. Векторные линии векторного поля ( ) будут перпендикулярны эквипотенциальной пов-ти скалярного поля U.

– параметрическая запись линии уровня

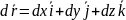при малых dx, dy, dz вектор 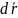также будет касательным в точке Р к линии L. и коллинеарны.

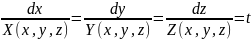
26. Поток, дивергенция векторного поля. Теорема Остроградского-Гаусса.

Задано вект поле в области V. В этой области задана пов-ть Q – двухсторонняя гладкая, замкнутая, ориентированная в направлении вектора нормали. Разобъем Q на 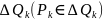пусть плоские, и на всей подобласти .

–кол-во жидкости, кот протекает за единицу времени через подобласть в выбранном направлении .

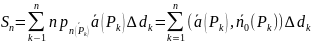Если диаметры и сущ предел интегральных сумм, то: 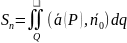Потоком П векторного поля через ориентированную пов-ть Q называют число, равное:

Дивергенция векторного поля. Задано вект поле . Пов-ть 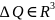замкнутая. Пусть 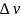– объем, кот ограничивает эта поверхность.

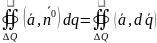Дивергенция векторного поля в точе Р ( ) – скалярная величина, равная пределу отношения потока векторного поля через замкнутую пов-ть к величине объема , ограниченного этой пов-тью при условии, что .

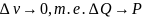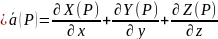Дивергенция хар-т мощность потока жидкости, исходящего из точки Р. Скалярная хар-ка, в отличие от потока – не суммарная, а в точке.

Т.О-Гаусса. Если векторн ф-я непрерывно дифференцируема в нек области V, кот ограничена замкнутой пов-тью Q, то: 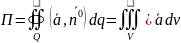. Поток вектора этого поля через пов-ть Q в направлении внешней нормали 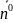равен тройному интегралу по области V по дивергенции.

26. Циркуляция и ротор векторного поля. Теорема Стокса.

Циркуляция. Рассмотрим 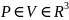. Рассм замкнутую кривую . . Циркуляция С векторного поля вдоль замкнутой ориентированной кривой L – число, равное значению линейного интеграла: ;

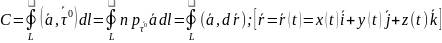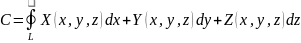
Ротор. – локальная векторная характеристика векторного поля, связанная с его вращательной способностью. Рассм , . Контур 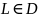; – площадь площадки, ограниченной контуром L.

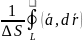– средняя циркуляция вект поля на площадке .

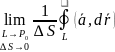– циркуляция векторного поля в точке .

Рассмотрим , ;

значение хар-т вращат способность в точке в направлении .

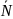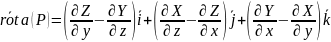
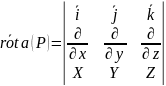
Теорема Стокса. Циркуляция С непрерывно дифференц вект поля по замкнутому положит ориентированному контуру L равна потоку ротора этого поля через любую гладкую пов-ть Q, опирающуюся на контур L.