26. Независимость криволинейного интеграла 2-го рода от пути интегрирования (случай плоской кривой). Нахождение ф-ии по ее полному дифференциалу.

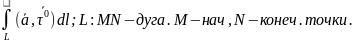
Рассмотрим криволинейный интеграл Предположим, что интеграл не зависит от пути интегрирования, тогда:

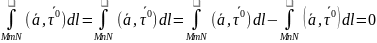
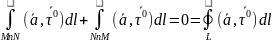
Если кривол интеграл не зависит от пути интегрирования, то интеграл по замкнутому контуру L ф-ии a равен 0.

Рассмотрим ;

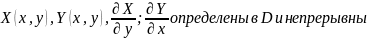
Теорема: если ф-ии определены и непрерывны в нек области D, то необходимым и достаточным условием независимости КРИ-2 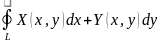является выполнение условия:

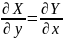
Нахождение ф-ии 2х переменных. – выполнение этого условия явл необх и дост условием того, что 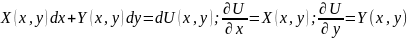интегрируем:

;

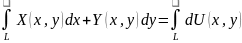
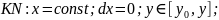
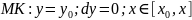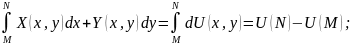
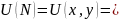
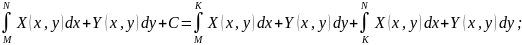где C=U(M);

5. Двойной интеграл. Определение, геометрический сымсл двойного интеграла.

Пусть в замкнутой области D плоскости Oxy задана непрерывная ф-я z=f(x,y). Разобъем область D на n элементарных областей 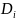, площади которых обозначим через 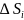, а диаметры – наибольшее расстояние между точками области – через .

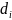эта сумма называется интегральной суммой ф-ии f(x,y) в области D.

Если существует конечный предел интегральной суммы, который не зависит от способа разбиения области и от выбора точек, то он называется двойным интегралом от ф-ии f(x,y) по области D и обозначается:

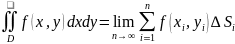
Геометрический смысл двойного интеграла состоит в том, что величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела.

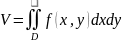
5. Свойства двойного интеграла.

1. 

2. 

3. 

4. Если то . Если , то

5. 

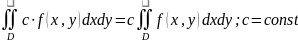
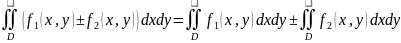
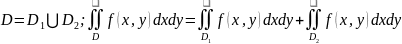
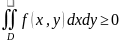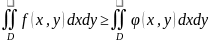
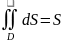
6. Если ф-я f(x,y) непрерывна в замкнутой области D, площадь которой S, то 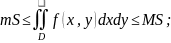где m, M соответственно, наименьшее и наибольшее значения подынтегральной ф-ии в области D.

7. Если ф-я f(x,y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка 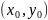, что . Величину 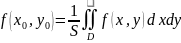называют средним значением ф-ии в области D.

5. Вычисление двойного интеграла в декартовых координатах.

Пусть требуется вычислить двйной интеграл , ф-я непрерывна в области D. Тогда двойной интеграл выражает объем цилиндрического тела, ограниченного сверху пов-тью z=f(x,y). Предположим сначала, что область D представляет собой криволин трапецию, ограниченную кривыми x=a, x=b и кривыми . Такая область – правильная в направлении оси Oy.

п остроим сечение цилиндрического тела плоскостью, перпендикулярной оси Ox: x=const. В сечении получим криволинейную трапецию ABCD, ограниченную линиями

площадь этой трапеции:

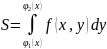
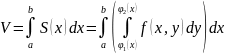
Объем также определяется как двойной интеграл от ф-ии f(x,y) по области D. Тогда:

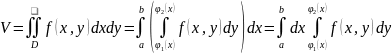
5. Приложения двойного интеграла в механике.

Масса плоской фигуры. Масса плоской пластинки D с переменной плотностью находится по формуле:

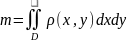
Статические моменты и координаты центра тяжести плоской фигуры.

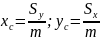
5. (+10). Замена переменных в двойном интеграле (+ двойной интеграл в полярных кординатах. Приложения двойного интеграла в геометрии).

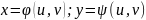если ф-ии имеют в некоторой области D* плоскости Ouv непрерывные чатсные производные первого порядка и отличный от 0 определитель: 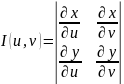-определитель Якоби – якобиан, а ф-я f(x,y) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:

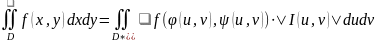
Рассмотрим частный случай замены переменных - замену декартовых координат x, y полярными координатами 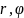. В качестве 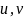возьмем полярные координаты . Они связаны с декартовыми координатами формулами . Правые части – непрерывно дифференц ф-ии. Якобиан определяется как:

Ф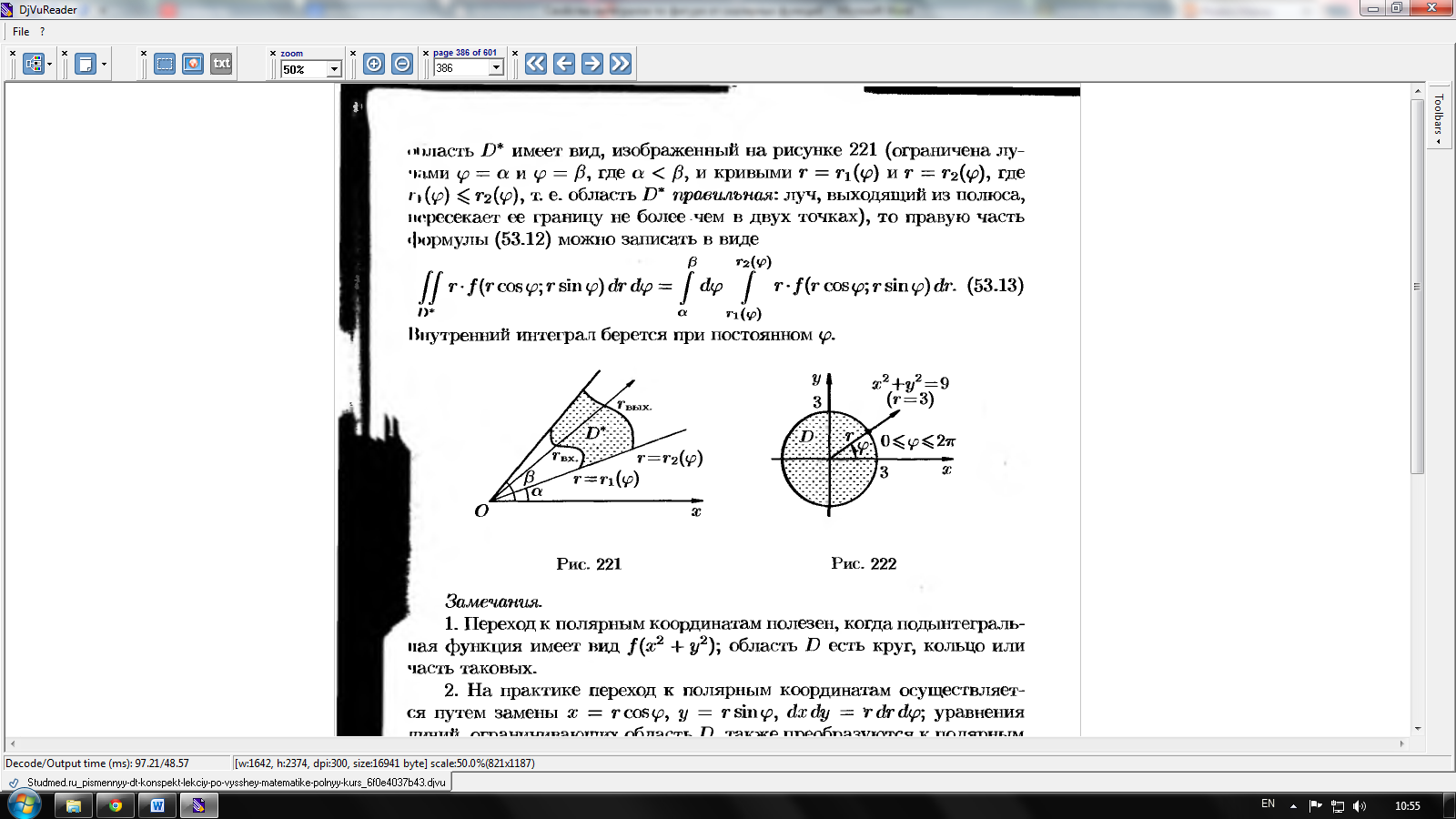 ормула замены переменных: . Для вычисления двойного интеграла в полярных координатах применяют правило его сведения к двукратному интегралу. Если область D* ограничена лучами и кривыми , то:

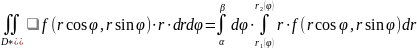
Приложения в геометрии:

Объем тела. - ур-е пов-ти, ограничивающей тело сверху.

Площадь плоской фигуры. Если f(x,y)=1, то цилиндр тело станет прямым цилиндром с высотой H=1. Объем численно равен площади основания S. Тогда