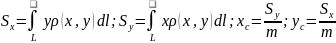- •Свойства интегралов по фигуре от скалярных функций.
- •Применение интегралов по фигуре от скалярной функции в геометрии.
- •Криволинейный интеграл 1 рода. Определение и простейшие свойства.
- •Вычисление криволинейного интеграла 1-го рода по кривой на плоскости в зависимости от способа задания кривой.
- •Вычисление криволинейного интеграла 1-го рода по кривой в пространстве.
- •Приложения криволинейного интеграла 1-го рода в механике и геометрии.
- •Поверхностный интеграл 1-го рода. Определение и простейшие свойства этого интеграла.
- •Вычисление поверхностного интеграла 1-го рода сведеением к двойному интегралу.
- •Приложения поверхностного интеграла 1-го рода в механике.
- •Интеграл по ориентированной фигуре от векторной функции. Теорема существования. Простейшие свойства.
- •Независимость криволинейного интеграла 2-го рода от пути интегрирования (случай плоской кривой). Нахождение ф-ии по ее полному дифференциалу.
- •Двойной интеграл. Определение, геометрический сымсл двойного интеграла.
- •Свойства двойного интеграла.
- •Вычисление двойного интеграла в декартовых координатах.
- •Приложения двойного интеграла в механике.
- •Тройной интеграл. Определение и простейшие свойства тройного интеграла.
- •В ычисление тройного интеграла в декартовых координатах. Приложения тройного интеграла в геометрии.
- •Тройной интеграл в сферических координатах.
- •Тройной интеграл в цилиндрических координатах.
- •Приложения тройного интеграла в механике.
- •Скалярное поле. Поверхности и линии уровня скалярного поля.
- •Производная по направлению. Градиент.
- •Векторное поле. Векторные линии и их уравнения.
- •Поток, дивергенция векторного поля. Теорема Остроградского-Гаусса.
- •Циркуляция и ротор векторного поля. Теорема Стокса.
- •Потенциальное векторное поле. Нахождение потенциала.
- •Соленоидальное и гармоническое векторные поля и их простейшие свойства.
- •Числовые ряды. Сходимость и сумма рядов. Простейшие свойства рядов. Необходимое условие сходимости числового ряда.
- •Знакопеременные ряды. Достаточный признак сходимости. Абсолютная и условная сходимости.
- •Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
- •Ряды с комплекными членами.
- •Функциональные ряды. Область сходимости. Понятие ранвомерной сходимости. Признак Вейерштрасса.
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус сходимости. Интервал сходимости.
Свойства интегралов по фигуре от скалярных функций.
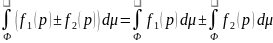
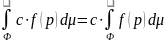 ;
c=const
;
c=const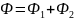 ;
;
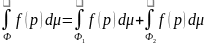
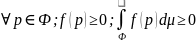

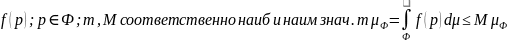 .
.
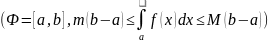
Теорема о среднем. Если f(p) определена и непрерывна на фигуре Ф и на ее границе, то найдется по крайней мере одна точка на этой фигуре, такая что справедливо равенство:
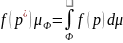

Применение интегралов по фигуре от скалярной функции в геометрии.
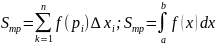


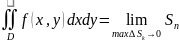
Рассмотрим задачу об объеме цилиндра.
 ;
;
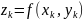 ;
;
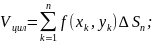
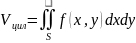 ;
;
 ;
;
Область D называется правильной (выпуклой) вдоль оси Х, если любая прямая, параллельная оси Х и пересекающая эту область, пересекает границу области не более 2х раз. Область правильная вдоль оси У – аналогично.
Предположим, что область D правильна дволь оси y. Отрезок AB является проекцией области D на ось Ox.
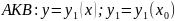
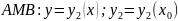
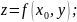
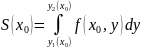
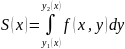
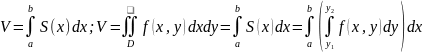
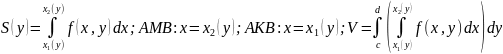 .
Т.о.
.
Т.о.
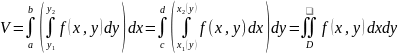
Криволинейный интеграл 1 рода. Определение и простейшие свойства.
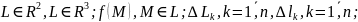
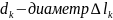

Если
сущ предел интегральных сумм
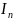 при условии, что
при условии, что
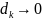 и этот предел не зависит от способа
разбиения кривой и от выбора точек
и этот предел не зависит от способа
разбиения кривой и от выбора точек
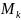 ,
то этот предел – криволинейный интеграл
по скалярной функции по кривой L
(криволинейный интеграл 1-го рода).
,
то этот предел – криволинейный интеграл
по скалярной функции по кривой L
(криволинейный интеграл 1-го рода).
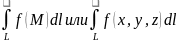
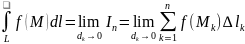
f(M)
интегрируемая ф-я по кривой L.
В каждой точке ф-я
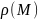 – плотность распределения масс.
– плотность распределения масс.
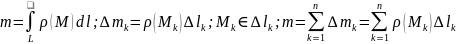

Свойства:
Пусть
 интегрируемы по кривой L.
интегрируемы по кривой L.
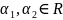 .
Тогда:
.
Тогда:
 также интегрируема по кривой L.
также интегрируема по кривой L.
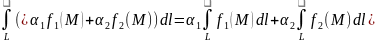 .
Свойство линейности.
.
Свойство линейности.Аддитивность.
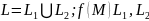 .
.
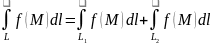
Если
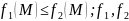 интегрируемы
по кривой L,
то
интегрируемы
по кривой L,
то
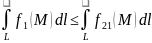
Теорема о среднем. Если непрер ф-я f(M) интегрируема по ограниченной связной замкнутой линии L, существует такая точка
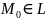 ,
что:
,
что:
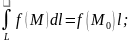 l
– длина кривой.
l
– длина кривой.
Вычисление криволинейного интеграла 1-го рода по кривой на плоскости в зависимости от способа задания кривой.
Пусть L задана явно уравнениями: y=y(x) – непрер диффер ф-я.
 .
.
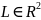 ;
;
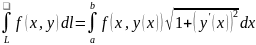
Если кривая L задана параметрическими уравнениями x=x(t), y=y(t),
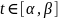 .
Где x(t)
y(t)
– непрер диффер ф-ии параметра t,
то:
.
Где x(t)
y(t)
– непрер диффер ф-ии параметра t,
то:
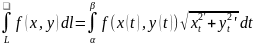
Если кривая L задана уравнением
 в полярных координатах, то
в полярных координатах, то
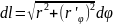 и
и
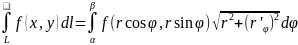
Вычисление криволинейного интеграла 1-го рода по кривой в пространстве.
L
гладкая и задана:
 . разобъем отрезок
. разобъем отрезок
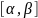 на n
частей, так что
на n
частей, так что
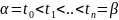 .
.
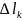 -
длина отрезка кривой. И найдется такая
точка t=
-
длина отрезка кривой. И найдется такая
точка t= ,
что
,
что
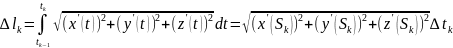
Выберем
точку
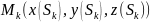 ;
;

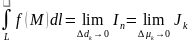
 – диаметр
отрезка
– диаметр
отрезка
 .
.
 – если
кривая задана параметрически. Очевидно,
что:
– если
кривая задана параметрически. Очевидно,
что:
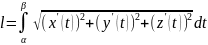 – длина кривой L.
– длина кривой L.
Приложения криволинейного интеграла 1-го рода в механике и геометрии.
Длина
кривой.
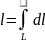
Площадь
цилиндрической поверхности. Если
направляющей цилиндрической поверхности
служит кривая L,
лежащая в плоскости Oxy,
а образующая параллельна оси Oz,
то площадь поверхности, задаваемой ф-ей
z=f(x,y),
находится по формуле:
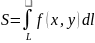 .
.
Масса
кривой.
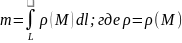 – плотность кривой в точке M.
– плотность кривой в точке M.
Статические моменты, центр тяжести. Статические моменты относительно осей Ox, Oy и координаты центра тяжести материальной кривой L определяются по формулам: