3. Решение неоднородных рекуррентных уравнений по виду правой части
В некоторых частных случаях частное решение можно найти по виду правой части уравнения (6.1).
3.1.
Пусть правая часть
является многочленом степени m
над полем
.
Тогда, если 1 не является корнем
характеристического уравнения, то
частное решение
будем искать, положив
причем коэффициенты
найдем,
подставив
в уравнение (6.1).
Если
1 является корнем характеристического
многочлена и кратность равна s,
то частное решение
будем искать исходя из условия
.
3.2.
Предположим, что
,
,
а
– многочлен степени
.
Если
не является корнем характеристического
многочлена
,
то частное решение
будем
искать, положив,
где
– многочлен степени не выше, чем
.
Если
– корень кратности s
характеристического
многочлена
,
то частное решение будем искать в виде
последовательности
,
где
,
где
– многочлен над
степени не выше, чем
.
3.3. К случаям 3.1 и 3.2 можно прийти на основании предложения 6.3.
Примеры.
1. Найдите общее решение уравнения
и
,
.
Решение. Составим однородное рекуррентное
уравнение, соответствующее данному:
Его характеристическое уравнение
имеет корни
,
.
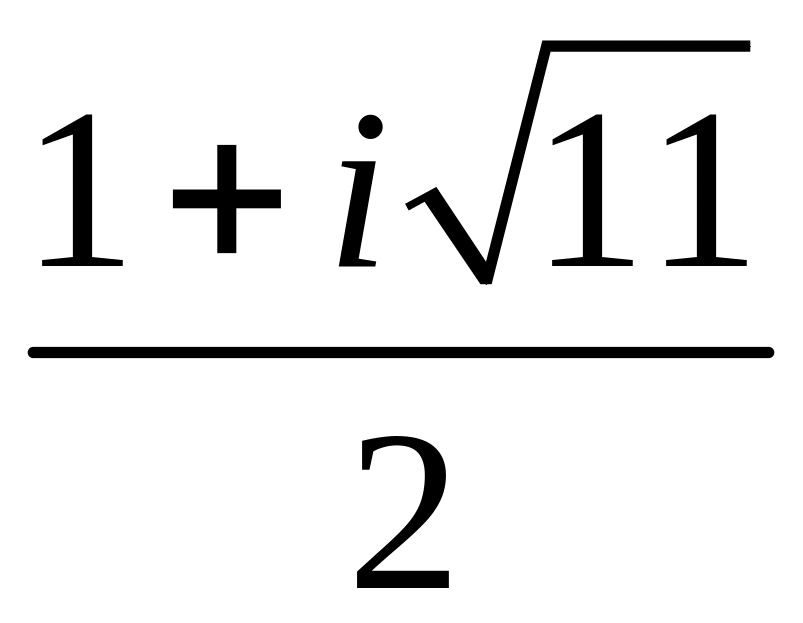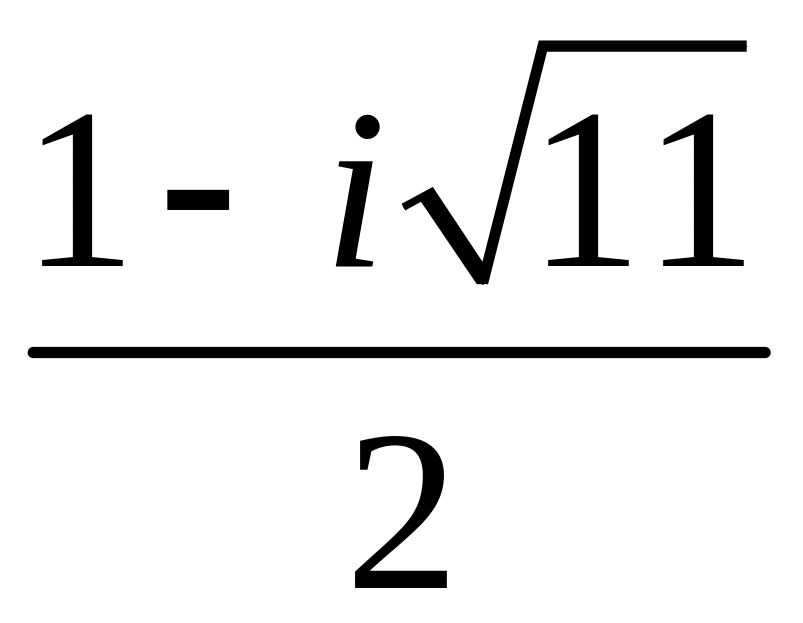Общее решение однородного уравнения
запишем в следующем виде:
,
где
.
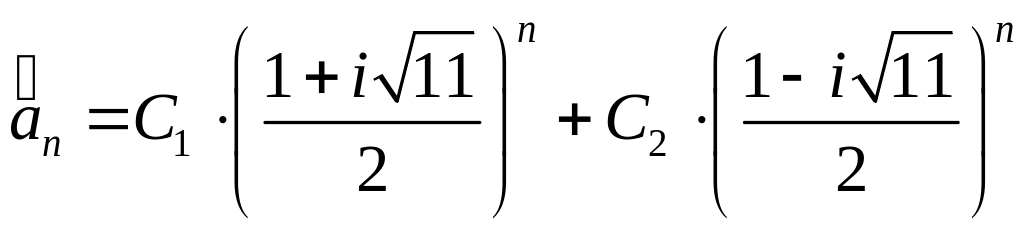По виду правой части
частное
решение
исходного уравнения будем искать в виде
многочлена первой степени:
так
как 1 не является корнем характеристического
уравнения.
Подставим частное решение в исходное
уравнение и найдем
и
:
отсюда, в силу того, что это равенство
должно выполняться при любом
находим
,
.
Окончательно общее решение данного неоднородного уравнения имеет вид:
2. Найдите общее решение рекуррентного уравнения над полем :
Решение. Общим решением однородного уравнения, соответствующего данному,
является последовательность
где
поскольку
корнями характеристического многочлена
являются числа 1, 2, и 3.
Так как 1 является корнем кратности 1, то общий член частного решения будем искать в виде многочлена:
.
Тогда
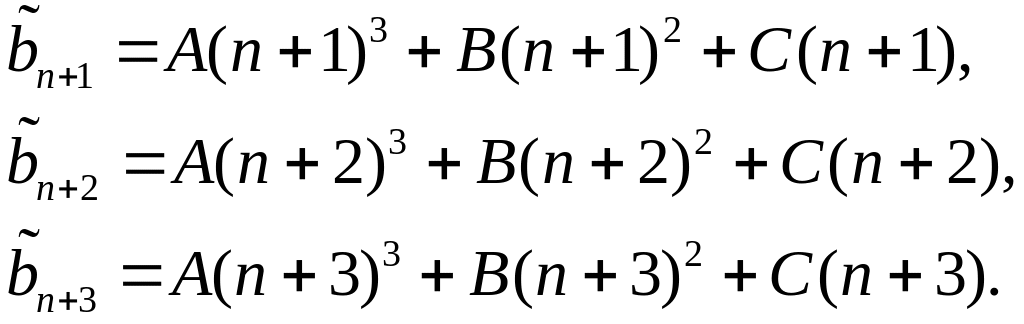
Подставим их в исходное рекуррентное уравнение:
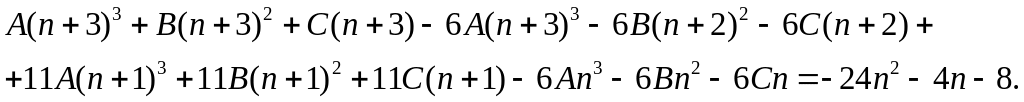
Раскрыв
скобки и сгруппировав подобные слагаемые,
получим систему уравнений относительно
коэффициентов
,
,
.
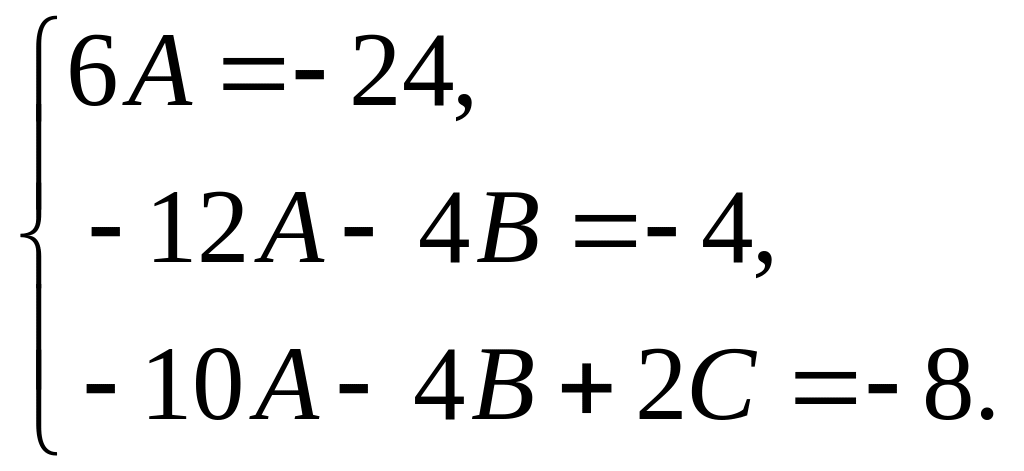
Отсюда общее решение определяется условием:
3. Найти общее решение рекуррентного уравнения над полем :
Решение. Характеристический многочлен
соответствующего однородного уравнения
имеет вид
Корнями этого многочлена являются числа
2 и –4, поэтому общее решение
определяется условием
Составим два неоднородных рекуррентных уравнения
(*)
(**)
Поскольку 1 не является корнем
характеристического уравнения
,
то частное решение
уравнения
(*) будем искать, исходя из условия
Тогда, подставив в (*), получим
Отсюда найдем
Решив эту систему, получим
.
Значит,
.
Число 2 является простым корнем
характеристического многочлена
,
поэтому частное решение
уравнения (**) будем искать, исходя из
условия
Подставив
в (**), получим
.
Отсюда,
.
Тогда общее решение исходного уравнения будет иметь вид:
.
Задачи
Решить следующие линейные неоднородные рекуррентные уравнения
.
.
.
.
.
.
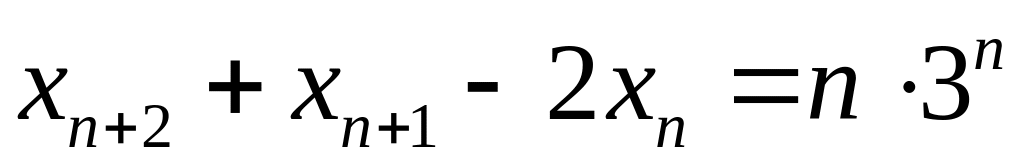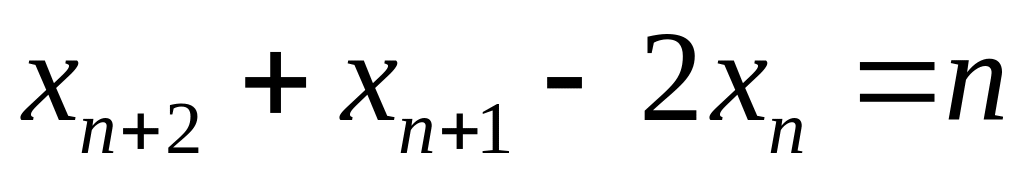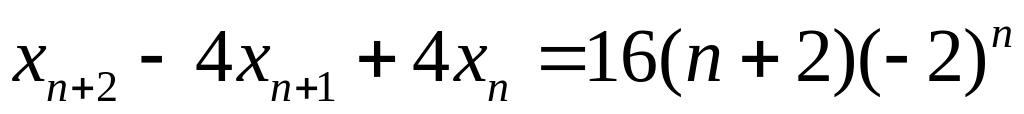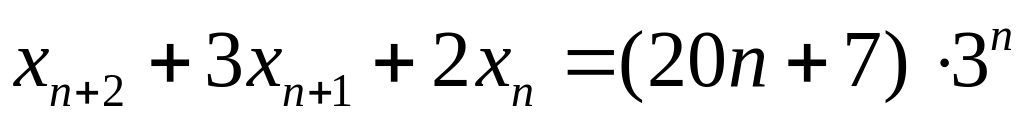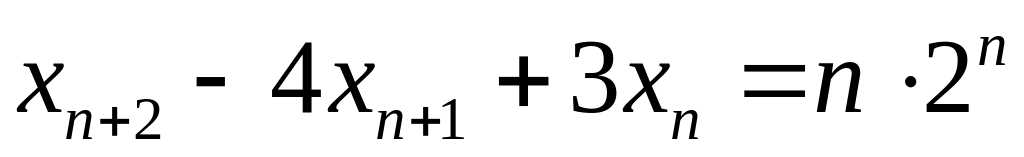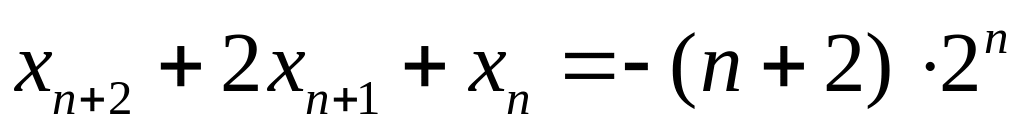