6.Средняя арифметическая, ее виды и методы расчетов. Математические свойства средней арифметической.

Средняя арифметическая вариационного ряда, сумма произведений всех значений признака на соответствующие частоты деленная на сумму частот. , где ni-соотв-я частота; n- кол-во вариантов в вариационном ряду; Wi-часности вар-в. Для не сгруппированного вар-го ряда рассчитывается простая средн. арифметическая ;

Свойства средней арифметической: 1)средн.арифмет. постоянной равна самой величине 2)если все варианты Хi увеличить (уменьшить) на одно и тоже число С, средн. ариф. увеличится (уменьш.) на тоже число 3) если все варианты Хi увеличить (уменьшить) в а раз, то увел. (уменьш.) в тоже число раз 4) ср. ариф. отклонений вар-в равна 0 5) средн. ариф. алгебраической суммы признаков равна ср. ар. этих признаков ; 6) если ряд состоит из нескольких групп общ.ср=общ.ариф.гр-х средних причем весами яв-ся объем группы

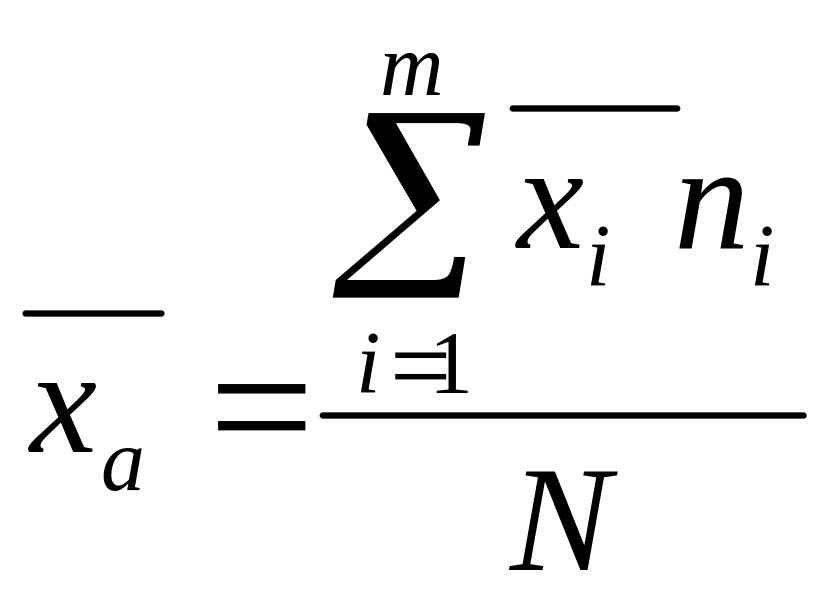
7.Средняя гармоническая, ее виды и способы расчета. Средняя геометрическая и средняя квадратическая.

При расчете средней по интервальному вариационному ряду х_i — середина интервала..

Средняя гармоническая взвешенная: , где w_i = x_i  f_i

Средняя геометрическая: невзвешенная: х =

где k — количество осредняемых величин;

Средняя квадратическая взвешенная х² =

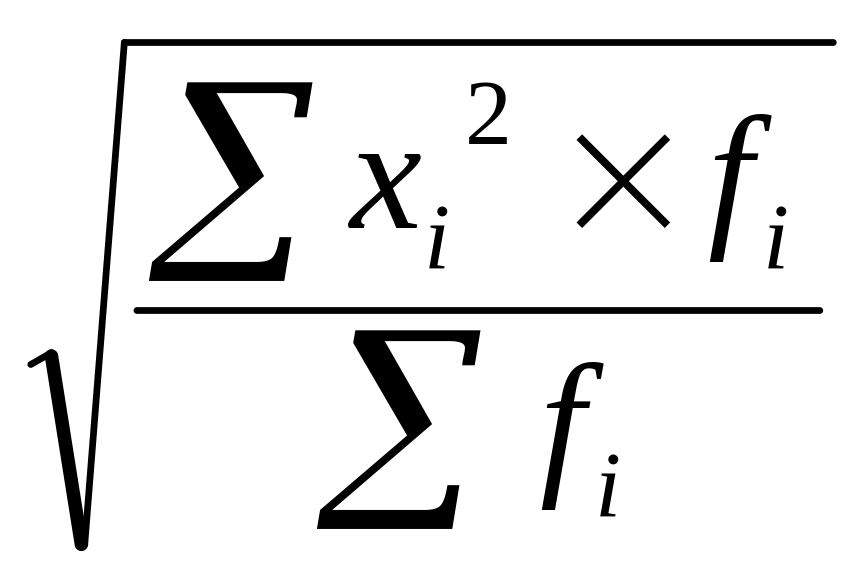
Формула средней геометрической используется чаще всего при расчете среднего значения по индивидуальным относительным величинам динамики, применяется когда индивидуальные значения признака заданы как относительные величины (темп роста)

Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени.

Среднюю квадратическую применяют если признаки измеряются в квадрате.

8.Мода и медиана. Соотношения между средней арифметической, модой и медианой. Ассиметрия.

Мода (М_о) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой (M_e) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Мода для дискретных рядов распределения отыскивается сразу (по максимальной частоте). Для определения медианного значения признака находят номер медианной единицы ряда (N_Me):

где n — объем совокупности.

Определение моды и медианы по интервальным рядам требует проведения расчетов на основе следующих формул:

, где х_o — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); h — величина модального интервала; f_Mo — частота модального интервала; f_Mo-1 — частота интервала, предшествующего модальному; f_Mo+1 — частота интервала, следующего за модальным.

, где х₀ — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); h — величина медианного интервала; S_me-1 — накопленная частота интервала, предшествующего медианному; f_Me — частота медианного интервала.

Между средней арифметической (`x ), медианой (Me) и модой (Mo) существуют определенные соотношения, позволяющие определить каждую из этих величин, если известны числовые значения двух других. Соотношение эти следующие: