19 Вопрос.Разделительно –категорические ,условные силлогизмы.
Разделительным называется УМЗ, в котором одна или несколько посылок - разделительные суждения.
Разделительно - категорическое УМЗ - когда одна посылка - разделительное суждение, другая - простое категорическое суждение. Есть 2 модуса :
1 модус - утверждающе-отрицающий. Союз "или" в этом модусе употребляется как в виде строгой, так и нестрогой дизъюнкции. "Данный глагол может стоять или в настоящем, или в прошедшем или в будующем времени. Данный глагол стоит в настоящем времени. Он не стоит ни в будующем, ни в прошедшем времени".
2 модус - отрицающе-утверждающий. "Минеральные удобрения бывают или азотными или фосфоритными или калийными. Данное удобрение не является не азотным, ни фосфорным. Данное удобрение калийное".
20.Вопрос Получение всех следствий из данных посылок.
Получение следствий из данных посылок
Получение всех следствий из посылок
Допустим, есть несколько посылок. Какие возможны заключения их этих истинных посылок?
1) Составляем конъюнкцию всех посылок
2) Находим СКНФ
3) Выписываем из СКНФ все возможные варианты комбинаций сомножителей (2n - 1, где n - количество этих сомножителей)
Пример:
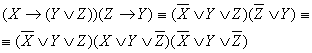
Возможные следствия:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
Доказательство, что любое из выражений является заключением
Все посылки истинны => их конъюнкция истинна => СКНФ - истинна, т. к. получаем равносильными преобразованиями => такое возможно, если истинны все сомножители => любой сомножитель (либо их комбинация) будет являться заключением.
Получение следствий, содержащих заданные переменные
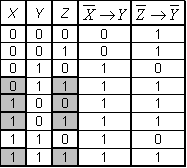
1) Составляем таблицу истинности
2) Подчёркиваем строку, где одновременно истинны все посылки
3) Подчёркиваем значения заданных переменных в этих случаях
4) Составляем СДНФ по выделенным строкам, учитывая только заданные переменные
5) Упрощаем СДНФ
П
ример:
