11. вопрос .

ЛОГИКА ВЫСКАЗЫВАНИЙ, раздел логики, в котором вопрос об истинности или ложности высказываний рассматривается и решается на основе изучения способа построения высказываний из т.н. элементарных (далее не разлагаемых и не анализируемых) высказываний с помощью логических операций конъюнкции ("и"), дизъюнкции ("или"), отрицания ("не"), импликации ("если..., то...") и др. Логику высказываний, задаваемую системой постулатов (аксиом и правил вывода), называют исчислением высказываний.

Семантика логики высказываний-в логике высказываний суждение не разделется на субъекты –предикаты,а рассматрив как простое из которого с помощью логич операции строится сложное суждение (высказывание)

В начале мат лог был создан симв язык,-язык формул.

ВЫСКАЗЫВАНИЕ- мысль, выраженная повествовательным предложением и могущая быть истинной или ложной.

1.конъюнкци(и) х*у (и ,а,но)

2.Дизъюнкция (или) X v Y(или)

3. Импликация a => b

4.эквиваленция(равнознач)- a => b (тогда и только тогда когда а)

5.Сумма по модулю 2 x+y

6 Инверсия ,не x черточка над х (неверно,что х..)

Особое место занимет импликация

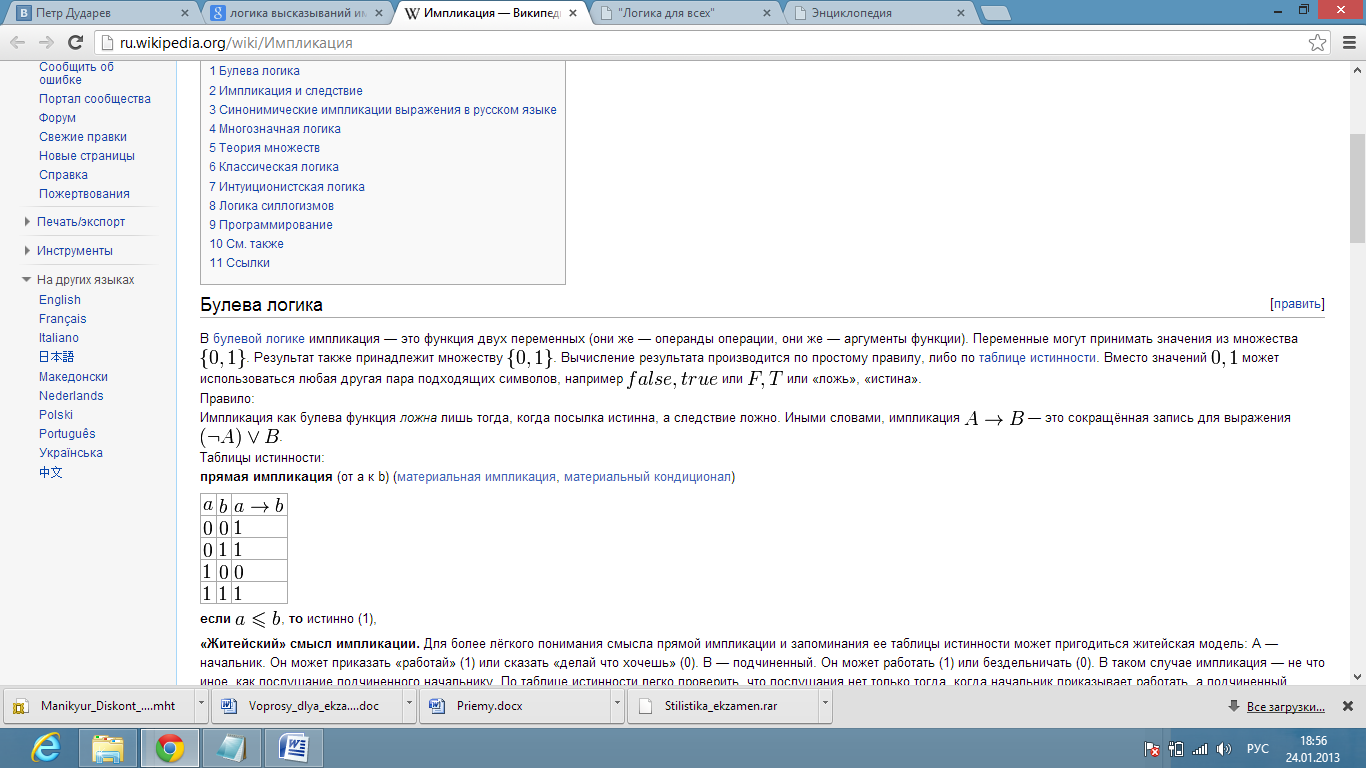
Св-во импликации-

1.х=>1=-xV1=1

2.0=>y=-0V-y=1Vy=1

3.x=>0=-x

Другие лог операции:

• Символы лог операции-пропозиционал знаки

• Символы переменных-пропозиционал переменых

• Совокупн символов операции и символов переменных образует семантику л.в.

Семантика-обозначающий

12.Вопрос Законы аристотеля

В основе л в лежат законы аристтотеля формализ Дж Булем.

1. Закон тождественности.                 А является  А.

Некоторый объект всегда равен самому себе. Некоторое суждение выражает само себя.

 

2.Закон противоречия. А не является не А.

Какой то объект не может одновременно иметь и не иметь какие-то свойства. Суждение не может быть одновременно и  истинным и ложным.

 

3. Закон исключения среднего. А не является

одновременно и А, и не А.

Некий объект или обладает, или не обладает некоторым свойством. Суждение может быть или истинным или ложным.

4. Закон достаточного основания Сущность закона: всякая мысль может быть признана истиной только тогда, когда она имеет достаточное основание, нсякая мысль должна быть обоснована.(Коммутатив,ассоциативность,дистрибутив,двойного отрицан,деморгана,идентпотентновсти,склеивания,поглощения)

13.Синтаксис Логики высказываний.

Описания Л В служит язык искуств языки для научн целей показывают формал языками.

Язык=>синтаксис (правило опред правильн слова называем формулами)

1.Алфавит Л В

-высказыва или пропозииционал перемен (X,Y,Z,X1,Y2….)

-Логич конст:(Истина,ложь;1,0)

-Знаки логич операц (&,V,=>,,(+), и др)

2.Определение формулы(ф)

-всякая высказыван переменная-формула

-всякая логич конст-формула

-если F1 u F2 формулы ,то F1*F2 ,F1VF2,F1=>F2 b итд где F связан логич операц также явл формулами с помощью формулы формализующ высказывания

3.Формализ высказываний

Закл в замене сложноо высказывания некоторой формулой

в Л В существ 3 типа формул:

-Ф наз выполнимой-если существ интерпритация при которой ф-истина

-Ф наз не выполним –если такой интепритац нет

-Ф наз тождественно истинной общезнач если она истина при любой интепритации

Поиск тождеств истиных формул одна из задач логики

14 Вопрос. Логическая равносильность.

2 высказыван равносильны если одновр истинны или ложны.2 формулы равносильны если их эквиваленция явл тавтологией F1F2=1

Логика высказываний-закон лог в том числе закон булевой алгебры изучены в курсе ДМ

Равносильность формул.

АиВ м б доказана (А=>B)&(B=>A)=1

Несколько тождеств равн форм.

Л В использ тождеств истин формулы (тавтологии) иногда наз законами логики иогда дополнит тавтологией

1.PQ=>Q-Конънкция сильннее каждого из его членов

2.P=>(PVQ)-Дизъюнкция слабее…

3.P=>(Q=>P)-Истина из чего угодно

4.-P=>(P=>Q)-Из ложного все что угодно

Доказываются путем равносильн преобразований.

1.PQ=>-PQvP=-Pv-QvP=1v-Q=1

2.P=>(PvQ)=-PvPvQ=1Vq=1

………………………………..

Формула Л В представ в формах:

-Днф

-Кнф

-Скобочная(смешаная)-как правило образует после формализации

-литера,литерал-элемент высказыв или его отрицание (буква или буква с инверс)

-Дизъюнкт-дизъюнкция конеч числа литералов,тоже что и плауза

15.Вопрос Способы доказательств общезначимости формул.Доказательство методом построения дерева редукции.

ормула A логики предикатов называется выполнимой в области M, если существуют значения переменных, входящих в эту формулу и отнесенных к области M, при которых формула A принимает истинные значения.      Формула A называется выполнимой, если существует область, на которой эта формула выполнима.      Из предыдущего определения следует, что, если формула выполнима, то это не означает, что она выполнима в любой области.      Формула A называется тождественно истинной в области M, если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.      Формула A называется общезначимой, если она тождественна истинна на всякой области.      Формула A называется тождественно ложной в области M, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.      Из приведенных определений следует:      1. Если формула A общезначима, то она и выполнима на всякой области.      2. Если формула A тождественно истинна в области M, то она и выполнима в этой области.      3. Если формула A тождественно ложна в области M, то она не выполнима в этой области.      4. Если формула A не выполнима, то она тождественно ложна на всякой области.      В связи с данными определениями естественно выделить два класса формул логики предикатов: выполнимых и не выполнимых формул.      Отметим, что общезначимую формулу называют логическим законом. 

Доказат общезначимости формул

Может быть получена след способами: 1.Получить ТИ

2.Алгебрич путем равносил преобразов

3.Дерево редукции

4.Метод резолюции

Редукция-уменьшение,упрощение чеголибо в каком либо отношении