4.1.3. Шкалирование квантификаторов

Рассмотрим квантификаторы. Они служат для введения количественных и качественных мер для понятий и отношений. Например, "для всех", "существуют такие что", "очень редко", "быстро" и т. д. Обозначаются кодификаторы перевёрнутыми буквами. Существуют квантификаторы качественные ( Например, "много", "близко" ) и количественные. Квантификаторы качественные требуют шкалирования, а это проблема.

4.1.4. Семантические сети

Определение : Семантическая сеть – это ориентированный граф, вершины которого – понятия, а дуги – отношения между ними.

В качестве понятий обычно выступают абстрактные или конкретные объекты, а отношения – это связи типа : «это», «имеет частью», «принадлежит» и т. п. Характерной особенностью семантических сетей является обязательное наличие трех типов отношений:

• класс – элемент класса (оборудование – станок);

• свойство – значение (рабочее поле 600 х700);

• пример элемента класса (станок токарный – станок ТПК 125).

Различают несколько классификаций семантических сетей, связанных с типами отношений между понятиями.

1. По количеству типов отношений:

• однородные (с единственным типом отношений);

• неоднородные (с различными типами отношений).

2. По типам отношений:

• бинарные (в которых отношения связывают два объекта);

• n – арные (в которых есть специальные отношения, связывающие более двух объектов).

Наиболее часто в семантических сетях используются следующие отношения:

• связи типа «часть – целое» (например, «класс – подкласс», «элемент – множество»);

• функциональные связи (обычно эта связь определяется глаголами «производить», «влияет» …);

• количественные (больше, меньше, равно …);

• пространственные (далеко от, близко от, за, под, над …);

• временные (раньше, позже, в течение …);

• атрибутные связи (иметь свойство, иметь значение);

• логические связи (И, ИЛИ, НЕ);

• лингвистические связи и другие.

Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети, отражающей поставленный вопрос к базе.

Недостатком этой модели является сложность организации процедуры поиска вывода на семантической сети. Для реализации семантической сети существуют специальные сетевые языки: NET, SIMER+MIR и др. Широко известны экспертные системы, использующие семантические сети в качестве языка представления знаний – PROSPECTOR, CASNET, TORUS.

Частным случаем семантических сетей являются синтагматические цепи и RX-коды.

Основной единицей языка представления знаний являются тройки вида (xdy). Такие тройки принято называть элементарными синтагмами. Формулы, получающиеся из них за счет связывающих отношений или операций исчисления высказываний, называются синтагматическими цепями.

Любая синтагматическая цепь может быть изображена геометрически в виде сети, вершинам которой сопоставлены понятия или имена, снабженные или не снабженные квантификаторами (а также модификаторами и оценками), а дугам - отношения (а также императивы), которые могут быть снабжены квантификаторами (а также модификаторами, модальностями и оценками).

Над сетями можно ввести некоторую алгебру, соответствующую определенным преобразованиям над записями на ЯПЗ. Введем операции

• объединения,

• пересечения сетей,

• дополнения,

• пополнения.

Первые три операции – синтаксические, последняя – семантическая. Первые две операции носят обычный теоретико-множественный характер и совпадают с операциями такого же типа, которые обычно вводятся в теории графов. Две других – оригинальные.

Операция объединения сетей. Операция объединения сетей объединить две сети в единую сеть. Суть этой операций следующая. Пусть даны две сети S1 и S2 (см. рис. 15). Результат S=S₁∪S₂ представляет собой сеть, состоящую из множества вершин сети S₁ и сети S₂ и множества отношений сети S₁ и сети S_2.

Операция пересечения сетей. Операция пересечения сетей позволяет выделить общие части этих сетей. Суть операции следующая. Пусть даны две сети S1 и S2 (рис. 15). Результат S=S₁∩S₂ представляет собой сеть, состоящую из пересечения множеств вершин сетей S₁ и S₂ и пересечения множеств отношений этих сетей_.

Операция дополнения сетей. Суть этой операции следующая. Пусть даны две сети S₁ и S₂ (рис. 16).

Рассмотрим первый случай, когда S₂⊂S₁ (см. рис. 16). Тогда дополнение сети S₂ относительно сети S₁ будет сеть, которая состоит из части сети S₁, в которую включаются вершины, не входящие в S₂, плюс те вершины S₂, которые соединены отношениями не входящими в S₂. Мы видим, что дополнение сети S₂ относительно сети S₁ не соответствуют операции дополнения теории множеств, так как в последнем случае мы бы имели сеть, представленную на рис. 17, но тогда пропали бы связи * и **, а их надо отразить. Поэтому берутся вершины X₄ и X₅.

Рассмотрим второй случай, когда S₂ и S₁ имеют вершины, не являющиеся общими (см. рис. 18). Тогда дополнение сети S₂ относительно сети S₁ будет определяться следующим образом. Первоначально определяется объединение сетей S₁ и S₂. Затем ищется дополнение сети S₂ относительно полученного объединения сетей.

Рассмотрим третий случай, когда S₂ и S₁ имеют все совпадающие вершины, но различные отношения между ними (см. рис. 19). В этом случае дополнение одной сети относительно другой также берется относительно их объединения.

В общем случае, операция дополнения сети S2 относительно сети S1 берется следующим образом:

• сначала определяется S2S1, а затем

• дополнение S2 берется относительно S2S1.

Рис. 15. Примеры операций объединения и пересечения

S₁

S₂

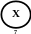
Дополнение сети S₂относительно S₁

*

**

Рис. 16 Пример операции дополнения

Рис. 17. Теоретико-множительное выполнения операции дополнения

S₁

S₂

Объединение S₁∪S₂

результат

Рис. 18. Пример операции дополнения

S₁

S₂

r₃

r₄

r₁

r₂

Объединение S₁∪S₂

результат

r₃

r₁

r₂

r₁

Рис. 19. Пример операции дополнения

Кроме чисто синтаксических операций для решения задач искусственного интеллекта служит операция пополнения, которая может быть как синтаксической, так и семантической. Отношение, если его рассматривать с алгебраической точки зрения, может, например, обладать каким-либо из трех свойств: рефлексивностью, симметричностью и транзитивностью.

Замечание: а) рефлексивность: xrx

б) симметричность: xry  yrx

в) транзитивность: xry и yrz  xrz

Если какое-либо из свойств не выполняется ни для одной пары, то отношения называются соответственно: антирефлексивным, антисимметричным и антитранзитивным.

Если относительно некоторого отношения известно, что оно обладает определенным свойством, то в записи в виде синтагматической цепи можно произвести пополнение с учетом этого свойства.

Например: Пусть задана технологическая операция, показанная на рисунке и представленная в виде сети.

r₂

r₂

r₂-быть раньше

r₂

Отношение r₂ в силу его семантики является транзитивным. Следовательно, сеть может быть пополнена отношениями, заданными пунктирными линиями.

r₂

r₂

r₂

Таким образом, суть операции пополнения состоит в достраивании описания реальных ситуаций с помощью некоторых формальных дедуктивных систем, отражающих наши знания о закономерностях проблемной области.

Существует специальный вид синтагматических цепей, применяемых при создании языков ИПС - это RX-коды. С их помощью некоторые понятия определяются через отношения с ранее определенными понятиями.

Например: пусть определены понятия:

d1 - разгрузка; d4 - схват;

d2 - загрузка; d5 - тележка;

d3 - передвижка; d6 - тара.

Тогда понятие "подвижного промышленного робота" можно определить как "элемент класса погрузочно-разгрузочных механизмов и приспособлений, служащих для погрузки и разгрузки".

RX-коды используются для хранения в модели знаний сведений о том или ином предмете или процессе. RX-коды - это статическое описание фактов проблемной области.

Синтагматические цепи и RX-коды представляют собой частный случай семантических сетей. Семантическая сеть в самом общем виде определяется как

C=<X₁,X₂,...,Xs,R₁,R₂,...R_q>,

где X₁,X₂,...Xs - некоторые зафиксированные множества,

R₁,R₂,...R_q - система отношений, определенных на множестве X. Отношения могут, в общем случае, быть n-арными.

Например: Пусть задана схема сборки в виде

В этой сети вершины - это детали или сборочные единицы. Отношения - это вхождения в сборку. Детали и сборочные единицы, входящие в один ярус сети, функционально независимы друг от друга и могут выполняться в любой последовательности. Пунктиром обозначено второе отношение - альтернативного включения.