Уравнение состояния идеальных и реальных газов.
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа устанавливает связь между макроскопической величиной - давлением, которое может быть измерено, например манометром, и микроскопическими величинами, характеризующими молекулу:
где р - давление, m0- масса молекулы, n - концентрация (число молекул в единице объема), V2 - средний квадрат скорости молекул.
Если через Е обозначить среднюю кинетическую энергию поступательного движения молекулы
можно записать:
Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.
Уравнение состояния
Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.
Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где
— давление,
— молярный объём,
— абсолютная температура,
— универсальная газовая постоянная.
Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка — объем молекул газа.
Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
Наиболее известны два способа получения уравнения: традиционный вывод самого Ван-дер-Ваальса и вывод методами статистической физики.
Традиционный вывод
Рассмотрим сначала газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет уравнению состояния идеального газа:
Далее предположим, что частицы данного газа являются упругими сферами одинакового радиуса r. Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b, которая, вообще говоря, зависит только от вещества, из которого состоит газ. Таким образом, получается следующее уравнение:
Стоит заметить, что вычитаемый объём b не будет в точности равен суммарному объёму всех частиц. Если частицы считать твёрдыми и абсолютно упругими шариками, то вычитаемый объём будет примерно в четыре раза больше. Это легко объясняется тем, что центры упругих шаров не могут приближаться на расстояние ближе .
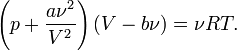
Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения:
Частицы распределёнными равномерно по всему объёму.
Силы притяжения стенок сосуда не учитываются, что в общем случае неверно.
Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга.
Внутренняя энергия, работа расширения, теплота процесса.
Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
где
— подведённое к телу количество теплоты, измеренное в джоулях
[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях
Эта формула является математическим выражением первого начала термодинамики
Для квазистатических процессов выполняется следующее соотношение:
где
— температура, измеренная в кельвинах
— энтропия, измеренная в джоулях/кельвин
— давление, измеренное в паскалях
— химический потенциал
— количество частиц в системе.
Работа расширения
Работа, производимая газом при расширении. Для бесконечно малого приращения объема dv она равна dW = pdv.
Вся работа при расширении от объема W, соответствующего начальному состоянию, до объема v2, соответствующего конечному состоянию, выражается определенным интегралом, где p есть функция υ, вид которой зависит от термодинамического пути. Р. Р. графически определяется на адиабатной диаграмме величиной площади, ограниченной сверху линией, изображающей зависимость p от v (переход тела из начального состояния в конечное) и ограниченной с боков двумя ординатами v1 и v2, а снизу — отрезком оси абсцисс.
Первый закон термодинамики.
Первый закон термодинамики.
Формулировка: В изолированной термодинамической системе сумма всех видов энергии является величиной постоянной.
Этот закон является частным случаем всеобщего закона сохранения и превращения энергии, который гласит, что энергия не появляется и не исчезает, а только переходит из одного вида в другой.
Из этого закона следует, что уменьшение общей энергии в одной системе, состоящей из одного или множества тел, должно сопровождаться увеличением энергии в другой системе тел.
Существуют другие формулировки этого закона:
1. Не возможно возникновение или уничтожение энергии (эта формулировка говорит о невозможности возникновения энергии ни из чего и уничтожения ее в ничто);
2. Любая форма движения способна и должна превращаться в любую другую форму движения (эта философская формулировка подчеркивает неуничтожимость энергии и ее способность взаимопревращаться в любые другие виды энергии);
3. Вечный двигатель первого рода невозможен. (Под вечным двигателем первого рода понимают машину, которая была бы способна производить работу не используя никакого источника энергии);
4. Теплота и работа являются двумя единственно возможными формами передачи энергии от одних тел к другим.
7) Энтальпия и энтропия.
Энтальпия.
В прошлом столетии Гибсс ввел в практику тепловых расчетов новую функцию - энтальпию.
Определение: Энтальпия - это сумма внутренней энергии тела и произведения давления на объем.
I = U + PV
Где:
I - энтальпия; U - внутренней энергия; P - давление; V - объем.
Удельная энтальпия i это отношение энтальпии тела к его массе.
Удельная энтальпия это параметр состояния.
Значение удельной энтальпии пара и воды при определенном давлении и температуре можно найти в справочнике. Пользуясь этими данными, можно определить количество теплоты участвующее в процессе или работу процесса.
Энтропия
Теплота q не является функцией состояния, количество теплоты выделившейся или поглотившейся в процессе зависит от самого процесса. Функцией состояния является энтропия обозначается S размерность Дж/К
dS = dQ/T
где:
dS 0 - дифференциал энтропии; dQ - дифференциал теплоты; Т - абсолютная температура;
Удельная энтропия отношение энтропии тела к его массе. Удельная энтропия s является справочной величиной.
Удельная энтропия - функция состояния вещества, принимающая для каждого его состояния определенное значение:
s = f (Р, v, Т) [Дж/кгЧ к]