6. Магнитные аномалии как ф-ции отображения параметров намагниченных источников. Интегральные представления д.Поверхностных и объемных источников.

П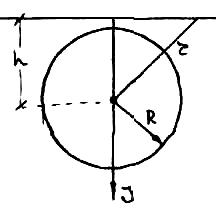 рямая задача-это расчет аномального магн. эффекта по известному геолог. разрезу. У геолог. разреза должны быть даны параметры магн. св-в и количеств. Размеры разреза Каждый магнит. источник залегает на своей глубине и обладает собственной намагниченностью, что и отражается в магн. поле-прямая задача в М/Р.. Между геолг. разрезом и распределением магн. аномалий существует тесная физико-математич. связь. Для вертикально намагниченного шара Z и H получат по формуле Пуассона:

U=-(J/f*)(V/z); где V-гравитационный потенциал,  -объем шара. V=f m/r, m-гравитац. масса.

Тонкий пласт (интегрируем шток)

Ф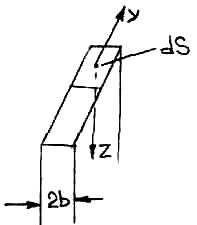 ормула для штока: Za=mh/(x²+h²)

Тонкий пласт 2b<<h

Тонкий пласт заменяется совокупностью штоков и записывают в трехмерном варианте с учетом простирания и паднеия. Дальнейшее интегрирование ведется по изменению угла видимости простирания пласта. Для вычисления эффекта для тонкого пласта, будем вести интегрирование по контуру, т.е. по линии, являющейся верхней границей. Нужно формулу для штока

проинтегрировать по оси Y в бесконечных пределах. И получим формулу:

Z=2J2bh/(x²+h²)

H=2J2bx/(x²+h²)

Мощный пласт – решение прямой задачи ведется путем интегрирования формулы тонкого пласта, который вырезается из мощного.

Z=2J;  -угол видимости верхней кромки

H=Jln(r₁^2/r₂²);

Z=2Jarctg(2bh/(x²-b²+h²)

H=Jln(x-b)+h²/(x+b)²+h²)

2b>>h

7. Магнитные аномалии как ф-ции совокупности параметров источников. Дифференциальный подход к решению прямой задачи.

7.8. Магнитные аномалии как функции совокупности параметров источников. Дифференциальный подход к решению прямой задачи. Соотношения, связывающие составляющие при косом и вертикальном намагничивании.

Полный вектор геомагнитной индукции связан зависимостью с вертикальной и горизонтальной составляющими . Полный вектор ориентирован по наклонению(I)МП и, следовательно, зависимость его при перемещении по профилю является сложной.

Если Z_n и Н_n – нормальные и Z_a и Н_a - аномальные значения, то

Угол между векторами равен разности наклонений. Отвеличины этой разности зависят величина аномального вектора Т_а и разность модулей Т-Т₀=∆Т. Считая что Т_i и Т₀ по направлению совпадают, существованием вектора Т_а можно пренебречь и можно написать следующую приближенную формулу:

Если учесть зависимость от наклонения можно написать:

График по профилю зависит от соотношения значений Z_a и Н_a. Влияние Н_a почтив три раза меньше, чем Z_a .

Прямую задачу в магниторазведке решают либо аналитическим, либо графическим способом. Прямая задача в силу известных свойств потенциала и его производных всегда имеет единственное и однозначное решение.

Решение прямой задачи основывается на предположении, что любое намагниченное тело можно рассматривать как систему бесконечно большого числа магнитных диполей с упорядоченно расположенными осями магнитных моментов. Тогда если объём намагниченного тела V, а вектор намагничения , то - магнитный момент бесконечно малого объема dV. В этом случае для потенциала U в точке p, находящейся на расстоянии r от элементарного объема dV намагниченного тела, можно записать

где вектор (grad1/r) направлен по r в сторону его возрастания. Если объем ограничен некоторой поверхностью s, тогда потенциал находим по формуле

I_n-проекция вектора намагниченности на внешнюю нормаль к поверхности.

Если тело является однородно намагниченным, то его магнитный потенциал определяется формулой

Если возмущающее тело имеет бесконечное простирание по одной из горизонтальных осей выражение для магнитного потенциала рассматривается в комплексной области. Комплексным магнитным потенциалом называется функция W(r)=U(r)+iV(r), где U(r)=ReW(r) – действительный потенциал; V(r)=I_mW(r) – функция потока.

Магнитный потенциал произвольно намагниченного тела определяется формулой

Формула Пуассона связывает магнитный потенциал с гравитационным. Для вертикально намагниченного шара Z и H получаем получаем по формуле Пуассона. Обозначая через V объем шара, гравитационный потенциал V и производную получаем по формулам ,

Далее по формулам Пуассона и Этвиша и учитывая что , получим ; ;

начало координат совмещено с центром шара. Шар вертикально намагничен.

Для косо намагниченного шара ,

где θ угол (J^r). Продолжив J до пересечения с координатной плоскостью xyz, получим точку Р(xyz) и её азимут А. Вводя углы φ и φ₀, используя основную формулу тригонометрии, выразив тригонометрические функции через прямоугольные координаты получим

если учесть, что φ=90^о-J, то формулы для косонамагниченного шара можно представить в виде ,

Аналогично выводятся формулы для других тел.