2. Показатели надежности восстанавливаемых систем

 

Все состояния системы S можно разделить на подмножества:

SK S – подмножество состояний j = , в которых система работоспособна;

S_M S – подмножество состояний z = , в которых система неработоспособна.

S = S_K S_M ,

S_K S_M = 0.

1. Функция готовности Г(t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t

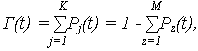
где Pj(t) – вероятность нахождения системы в работоспособном j-м состоянии;

Pz(t) – вероятность нахождения системы в неработоспособном z-м состоянии.

2. Функция простоя П(t) системы

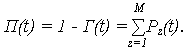
 3. Коэффициент готовности kг.с. системы определяется при установившемся режиме эксплуатации (при t ). При t устанавливается предельный стационарный режим, в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются

 Коэффициент готовности kг.с. можно рассчитать по системе дифференциальных уравнений, приравнивая нулю их левые части dP_i(t)/dt = 0, т.к. P_i = const при t . Тогда система уравнений превращается в систему алгебраических уравнений вида:

 

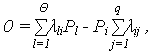
и коэффициент готовности:

 есть предельное значение функции готовности при установившемся режиме t .

4. Параметр потока отказов системы

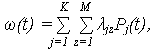
где _jz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.

5. Функция потока отказов

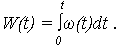
6. Средняя наработка между отказами на интервале t

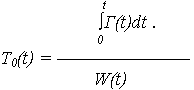
Последовательность выполнения работы

Исходная информация: - принципиальная схема энергоблока;

- средние наработки до отказа и среднее время восстановления элементов после отказа.

Часть 1. Моделируется ситуация: оба котлоагрегата подключены к главному паропроводу. Расход пара на турбоагрегат может быть обеспечен одним котлоагрегатом при его номинальной нагрузке.

Это позволяет рассматривать один из котлоагрегатов, как находящийся в в нагруженном резерве

Принципиальная схема энергоблока:

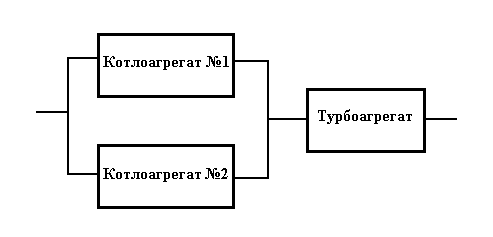
Граф состояний энергоблока: вариант горячего (нагруженного) резерва

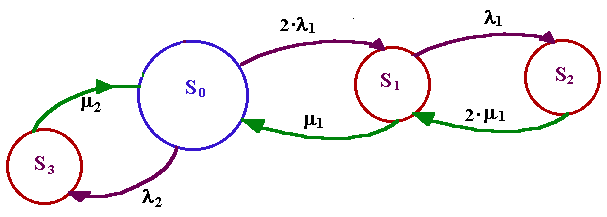
Состояния энергоблока: S₀ - работоспособное состояние энергоблока;

S₁ - отказ одного котлоагрегата;

S₂ - отказ двух котлоагрегатов;

S₃ - отказ турбоагрегата.

Среднее время безотказной работы (ч):

t₁ – среднее время безотказной работы котлоагрегата

t₂ – среднее время безотказной работы турбоаграгата

Среднее время восстановления (ч):

tv₁ – среднее время восстановления котлоагрегата

tv₂ – среднее время восстановления турбоаграгата

1. Вычисляем интенсивности отказов и восстановлений:

- интенсивности отказов;

- интенсивности восстановлений отказавших элементов.

2. Задаем вектор р начальных значений вероятностей нахождения объекта в каждом их четырёх состояний. (Сумма всех начальных значений должна быть равна единице.)

3. Строим систему дифференциальных уравнений перехода из одного состояния в другое

4. Решая систему дифференциальных уравнений, находим функции вероятностей нахождения системы в состояниях S0, S1, S2, S3

5. Определяем функцию готовности энергоблока при нахождении одного из котлоагрегатов в горячем резерве.

6. Определяем коэффициент готовности энергоблока при нахождении одного из котлоагрегатов в горячем резерве.