Последовательность выполнения работы

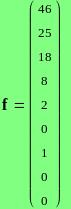
Исходная информация: выборка чисел (матрица А), представляющих собой наработки объектов и соответствующие количества отказов при этих наработках.

1.Вычисление средней наработки на отказ и среднеквадратического

отклонения:

_{- наработки, первая строка матрицы.}

- параметр b равен ширине интервала между соседними классами наработок.

_d=783 - величина d соответствует наработке в классе с наибольшим количеством отказов.

отклонение i-ой наработки от наработки с наибольшим количеством отказов.

_{- число отказов, вторая строка матрицы.}

_{общее число отказов}

- среднее значение наработки на отказ.

Вычисляем статистическая оценка среднеквадратического отклонения.

Строим гистограму по исходным данным:

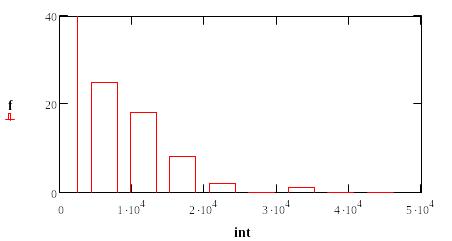
Проверка статистических гипотез:

Гипотеза №1: Распределение исходных данных о наработке до отказа

соответствует экспоненциальному закону.

Параметр экспоненциального закона λ корректируется путём изменения математического ожидания "x1" относительно среднего значения х исходной выборки на величину смещения Δ.

Вычисляем значения вероятности , случайных величин подчиняющихся экспоненциальному закону распределения, при наработках

Вычисляем частоту отказов при наработках

Строим гистограмму частот отказов при экспоненциальном законе распределения и полигон частот исходной выборки

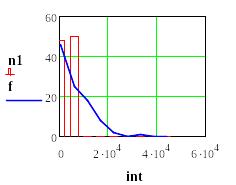
Критерий Хи-квадрат Пирсона при гипотезе экспоненциального закона распределения наработок до отказа:

Число степеней свободы

Доверительная вероятность

Вычисляем квантиль Хи -квадрат распределения при заданной доверительной вероятности и числе степеней свободы

Вычисляем среднеквадратичное отклонение статистических и вычисленных значений частот отказов

Сравнивая вычисленного значения критерия χ и значения квантили Х делаем вывод о верности гипотезы. Гипотеза экспоненциального закона распределения наработок до отказа может быть принята в случае если вычисленное значение меньше квантили.

Гипотеза №2: Распределение исходных данных о наработке до отказа

соответствует нормальному закону .

Число отказов при зафиксированных наработках объектов при нормальном

законе распределения равно:

Статистические оценки математического ожидания "x" и среднеквадратического отклонения "s" корректируются для получения согласия с проверяемой гипотезой на величину смещения Δ и D.

Вычисляем значения вероятности , случайных величин подчиняющихся нормальному закону распределения, при наработках

Вычисляем частоту отказов при наработках

Строим гистограмму частот отказов при нормальном законе распределения и полигон частот исходной выборки

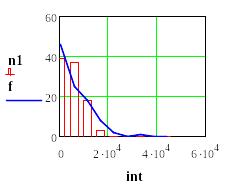
Критерий Хи-квадрат Пирсона при гипотезе нормального закона распределения наработок до отказа:

Число степеней свободы

Доверительная вероятность

Вычисляем квантиль Хи -квадрат распределения при заданной доверительной вероятности и числе степеней свободы

Вычисляем среднеквадратичное отклонение статистических и вычисленных значений частот отказов

Сравнивая вычисленного значения критерия χ и значения квантили Х делаем вывод о верности гипотезы. Гипотеза экспоненциального закона распределения наработок до отказа может быть принята в случае если вычисленное значение меньше квантили.

Гипотеза №3: Распределение исходных данных о наработке до отказа

соответствует закону Вейбулла

Параметры закона Вейбулла:

Число отказов при зафиксированных наработках объектов при нормальном

законе распределения равно:

Статистические оценки математического ожидания "x" и среднеквадратического отклонения "s" корректируются для получения согласия с проверяемой гипотезой на величину смещения Δ и D.

Параметр формы в распределении Вейбулла находятся по одной их формул в зависимости от значения коэффициента вариации

При коэффициенте вариации меньше единицы первая формула, а в противном случае - вторая.

- параметр масшаба в распределении Вейбулла;

Вычисляем значения вероятности , случайных величин подчиняющихся нормальному закону распределения, при наработках

Вычисляем частоту отказов при наработках

Строим гистограмму распределения частот отказов по закону Вейбулла и полигон частот исходной выборки

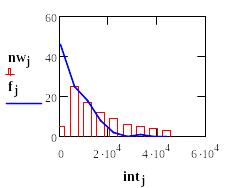
Вычисление критерия Хи-квадрат Пирсона распределения наработок до отказа по гипотезе закона Вейбулла:

Число степеней свободы

Доверительная вероятность

Вычисляем квантиль Хи -квадрат распределения при заданной доверительной вероятности и числе степеней свободы

Вычисляем среднеквадратичное отклонение статистических и вычисленных значений частот отказов

Сравнивая вычисленного значения критерия χ и значения квантили Х делаем вывод о верности гипотезы. Гипотеза экспоненциального закона распределения наработок до отказа может быть принята в случае если вычисленное значение меньше квантили.

Сделать выводы по работе:

1. Какими законами распределения, с какими параметрами, может быть представлена статистическая наработка.

2. Какими причинам отказов может быть описана рассмотренная статистическая наработка.