Последовательность выполнения работы
Исходная информация:
γ- доверительная вероятность;
N- число объектов выборки;
L - число отказавших объектов.
Вычисление вспомогательных величин:
k1=2L+2
k1=2L- число степеней свободы для вычисления квантилей χ2 распределения;
Вычисляем квантили χ1 и χ2 распределения χ2 для (γ, k1) и (1-γ,k2) используя функции qchisq(MathCAD), hi2inv (MathLAB), ХИ2ОБР (Excel)
Точечная оценка вероятности безотказной работы:
Вычисление нижней интервальной оценки вероятности безотказной работы:
Вычисление верхней интервальной оценки вероятности безотказной работы:
Вычисление нижней интервальной оценки вероятности безотказной работы при числе отказавших объектов равном нулю:
Исследовать:
1. Влияние величины доверительной вероятности на интервал гарантированной оценки вероятности безотказной работы.
2. Влияние числа отказов на размер области гарантированной оценки вероятности безотказной работы.
3. Рассмотреть при различной доверительной вероятности частный случай, когда число отказов L =0.
Результаты исследования отразить в выводах.
Выводы: 1. Вероятность безотказной работы анализируемых объектов находится в интервале от ... до .... Этот результат получен с доверительной вероятностью γ =....
2. Для повышения информативности оценки вероятности безотказной работы необходимо увеличить объём выборки исходных данных или определять закон распределения наработок до отказа, что требует новых исходных данных в виде наработок объектов до отказа.
3. С увеличением доверительной вероятности γ2=..... интервальные оценки становятся равными Pv= ..... Pn=.....
4. С изменением числа отказов L2=..... интервальные оценки становятся равными Pv= ..... Pn=.....
5. При числе отказов равном нулю ...
Контрольные вопросы
1. Что такое гарантированная оценка показателей надёжности?
2. Что является пределом верхней интервальной оценки Рv при доверительной
вероятности, стремящейся к единице?
3.Что является пределом нижней интервальной оценки Рн при доверительной
вероятности, стремящейся к единице?
4. Как будет выглядеть гарантированная оценка Р0 при числе отказов равном нулю?
5. Что такое доверительная вероятность?
6. Что такое интервальные оценки и доверительная область.
7. Каким образом получают выборку для проведения исследований надежности?
7. Что такое квантиль функции распределения случайной величины?
Лабораторная работа №2 «Определение закона надёжности невосстанавливаемых технических объектов по полностью определённой выборке» Теоретические основы
1. Экспоненциальное распределение
Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний (выходного контроля) отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации.
Эти
объекты можно отнести к «не стареющим»,
поскольку они работают только на участке
с
(t)
=
=
const. Круг
таких объектов широк: сложные технические
системы с множеством компонентов,
средства вычислительной техники и
системы автоматического регулирования
и т. п. Экспоненциальное распределение
широко применяется для оценки надежности
энергетических объектов.
Считается, что случайная величина наработки объекта до отказа подчинена экспоненциальному распределению, если ПРО описывается выражением:
f(t) =λexp( -λt),
где λ– параметр распределения, который по результатам испытаний принимается равным
λ
1
/
0
,
где 0 – оценка средней наработки до отказа.
Остальные показатели безотказности при известной f(t), определяются:
- вероятность безотказной работы (ВБР): |
P(t) = exp ( - λt), |
|
- вероятность отказа (ВО): |
Q(t) = 1 - exp ( - λt), |
|
- интенсивность отказов (ИО): |
(t) = λexp ( -λt) / exp ( -λt) =λ. |
|
ИО является постоянной величиной, не зависящей от времени наработки.
Числовые характеристики наработки до отказа определяются:
- средняя наработка (МО наработки) до отказа
- дисперсия наработки до отказа
Графики изменения показателей безотказности при экспоненциальном распределении приведены на рис. 1.
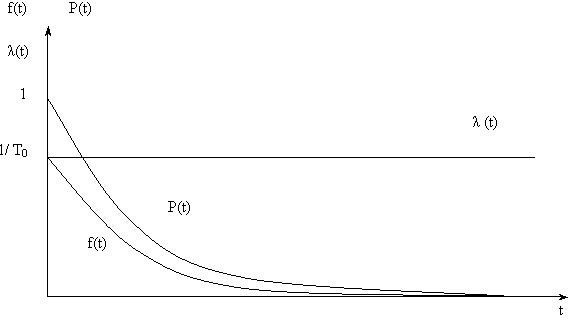
Рис. 1