3.2.3 Алгоритм видалення вузла

У даному алгоритму здійснені посилання на алгоритм пошуку вузла (розділ 3.2.1). Для зручності везол що видаляється позначимо - N, його батька - PN, вузол, що замінить N – C, його батька – PC. NIL – листки (їхня адреса NULL).

Крок 1

Пошук вузла що видаляється і його батька.

Крок 2

Якщо нащадки вузла N являються NIL, вузол N видаляється, PN на місце адреси N отримує адресу NIL, завершуємо виконання, інакше крок 3.

Крок 3

Якщо один з нащадків N є NIL, вузол видаляється, PN на місце адреси N отримує адресу нащадка, що не є NIL, завершуємо виконання, інакше крок 4.

Крок 4

Пошук C і PC, за іншим критерієм: замість пошуку за ключем виконується пошук по лівій вітці N рухаючись завжди у правий бік, доти, доки поточний вузол правим нащадком матиме NIL, цей вузол буде C. З C у N копіюються дані і ключ, з C і PC виконуються крок 2 або крок 3 (залежно від умови, що підходить під даний випадок, також для наступної команди вважається, що N=C, PN=PC).

3.3 Алгоритм вирішення задачі балансування

Основою вирішення задачі балансування являється створення алгоритмів та методів балансування і їх програмна реалізація. Для даної програми потрібно створити дві функції балансування: 1 – для балансування при додаванні елемента у дерево; 2 – при видаленні елемента з дерева. Алгоритми вирішення даних задач описані у матеріалах [3, 5], для додавання і [6, 7], для видалення. Вони базуються на основних закономірностях даної системи і оперують перемиканням зв’язків у системі для забезпечення виконання законів системи. Закони системи описані у підпункті «Червоно – чорні дерева» пункту «Вступ». Алгоритми балансування виконуються після здійснення операцій додавання чи видалення вузлів.

3.3.1 Алгоритм балансування при додаванні вузла

Для зручності позначимо вузли, що додали – N (при зміні N у алгоритмі, вважається що N це вітка з порушенням), його батько – P, його дідо (батько батька) – G, інший нащадок діда (дядько) – U. case_n (випадки), описані нижче.

Крок 1

Пошук вузлів N, P, G, U, надання N червоного кольору.

Крок 2

Перевіряємо чи виконується умова case_1, якщо так, виконуємо case_1, присвоюємо N=G і пере присвоюємо адреси вузлів P, G, U для нового N, повторюємо крок 2.

Інакше (якщо умова case_1 не виконалась) перевіряємо умову case_2, при істиній умові виконуємо case_2, інакше не виконуємо.

Крок 3

Виконуємо case_3, пере балансування завершено, завершуємо виконання.

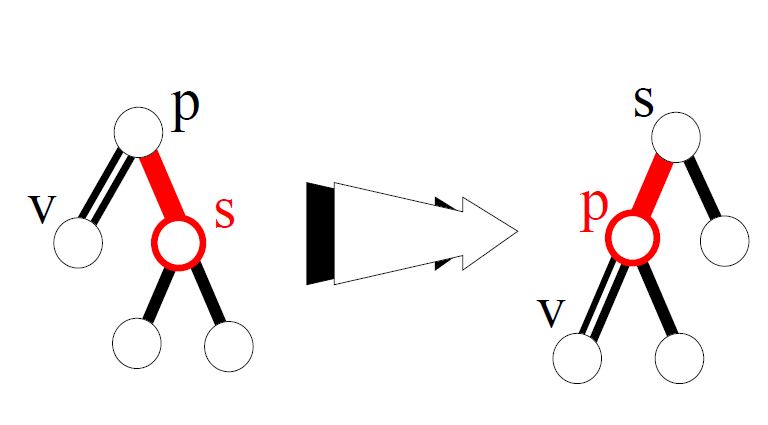
case_n це наступні випадки (зображені лівосторонні випадки, правосторонні аналогічні, тільки симетрично обернені):

Дані випадки перебудови зв’язків взяті з матеріалів наведених у джерелі [5].

case_1

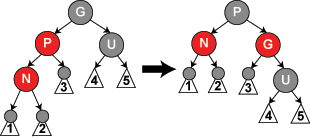
case_2

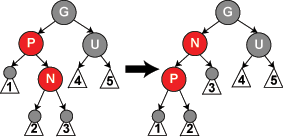
case_3

3.3.2 Алгоритм балансування при видаленні вузла

Балансування при видаленні вузла відбувається за аналогічним принципом, що і при додаванні вузла, тільки з іншими перестановками. V – вузол, що приєднався до батька видаленого вузла (при зміні значення V, вважається, що V це порушення, вітка V міститиму на один чорний вузол менше від інших), P – батько V, S – умовно брат V, інший нащадок P, Sl і Sr – лівий і правий нащадки S.

Крок 1

Якщо колір видаленого вузла був червоний, балансування не порушене, завершуємо виконання. Якщо колір видаленого вузла був чорний, а його нащадок не є NIL, і є червоного кольору, за правилами видалення цей нащадок заміняє його і отримує чорний колір, балансування не порушене, завершуємо виконання. Якщо вище наведені умови не виконуються, переходимо на крок 2.

Крок 2

Перевірка умови case_1, при істинній умові виконується case_1, балансування здійснено, завершуємо виконання.

Перевірка умови case_2, при істинній умові виконується case_2, балансування здійснено, завершуємо виконання.

Перевірка умови case_3, при істинній умові виконується case_3, балансування здійснено, завершуємо виконання.

Перевірка умови case_4, при істинній умові виконується case_4, пере присвоюємо V=P, тепер V – це вітка з порушенням, відповідно до V переприсвоюємо P, S, Sl, Sr, повторюємо крок 2.

Перевірка умови case_5, при істинній умові виконується case_5, пере переприсвоюємо P, S, Sl, Sr, відносно нового положення V, повторюємо крок 2.

Дані випадки перебудови зв’язків взяті з матеріалів наведених у джерелі [7].

case_1 і case_2

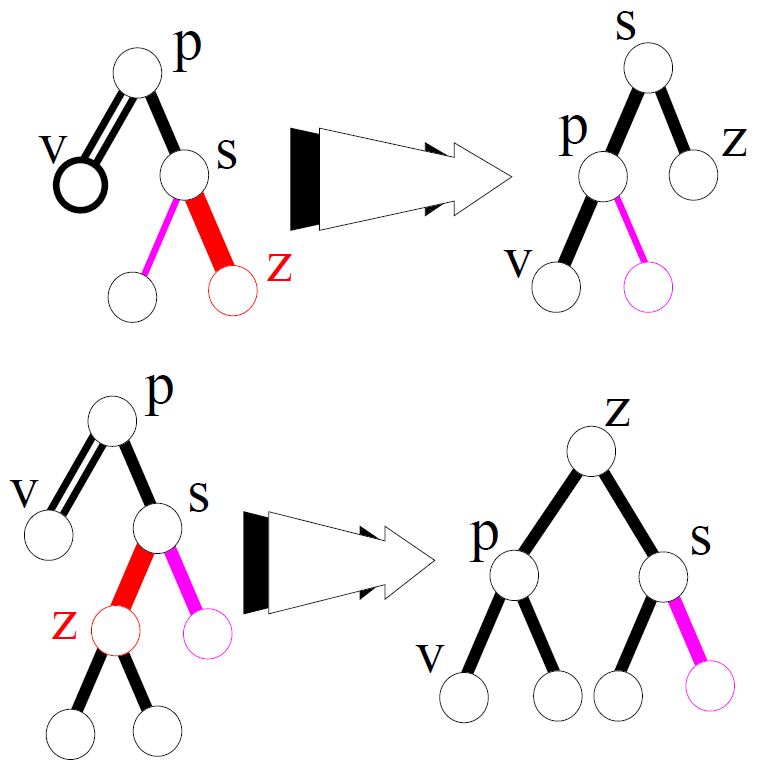
case_3 і case_4

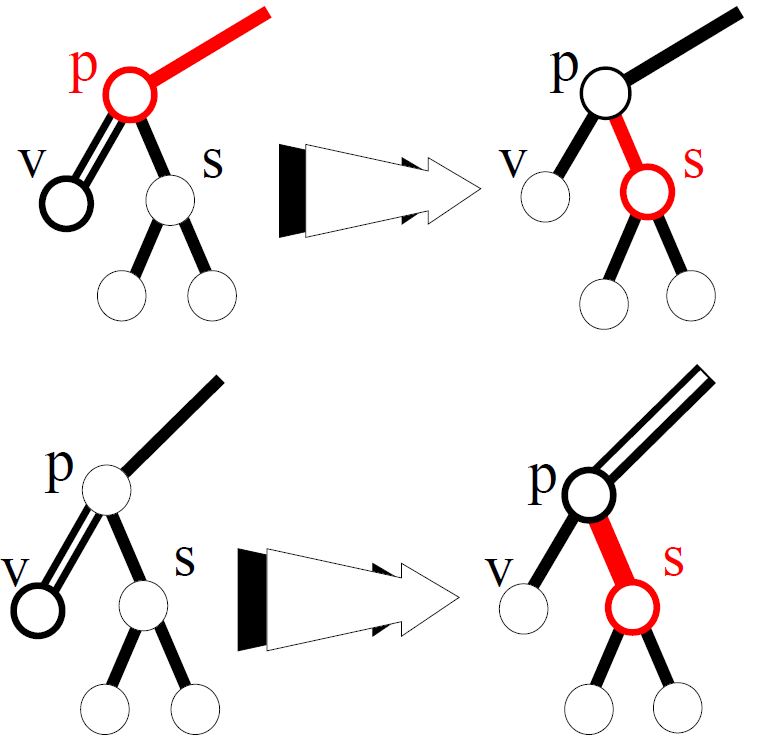
case_5