7. Что такое статистика? Качественные свойства статистик.
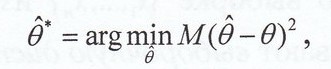
Как вычислить по выборке среднее, медиану и моду?
Основной
характеристикой случайной величины
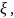определяющей
положение её центра распределения,
является математическое ожидание
.
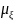Не зная функции плотности вероятности
,
нельзя точно вычислить и
. Поэтому по выборке
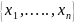из
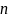независимых наблюдений случайной
величины
оценивают выборочное среднее
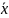
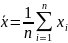
Математическое ожидание выборочного среднего равно
Значит статистика несмещенная . Можно доказать, что состоятельна и эффективна. Важные сведения о распределении - смотреть теорему Линдеберга!!!!!
Альтернативные выборочному среднему оценки положения центра распределения случайной величины - выборочные медиана и мода.
Для
оценки выборочной медианы нужно
построить вариационный ряд
,
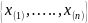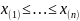, а затем взять либо
, если
нечетное число, либо
,
если
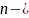четное.
Выборочная медиана является состоятельной и несмещенной оценкой математического ожидания . Она просто оценивается, при достаточно большом объеме выборки её распределение близко к нормальному распределению, однако эффективность медианы ниже, чем у выборочного среднего, так как её дисперсия более чем в полтора раза превышает дисперсию среднего.
Для оценки выборочной моды нужно из выборки , которая содержит повторяющиеся значения, выбрать значение с наибольшим числом повторений.
9. Как вычислить по выборке дисперсию, стандартное отклонение и размах.
Основной характеристикой рассеяния случайной величины q, является дисперсия
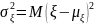
Плотность
вероятности
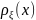обычно полностью не известна и
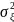нельзя вычислить точно. Поэтому по
выборке
из n независимых наблюдений
случайной величины
,
оценивают выборочную дисперсию
:
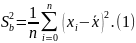
Эта статистика состоятельна и эффективна. Однако, как можно доказать,
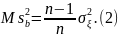
т.е. смещена, что и отражено индексом b.
Из (2)—го видно, как уточнить статистику , чтобы она стала несмещенной:
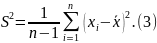
Хотя
отличие между статистиками
и
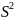невелико, особенно при больших n,
широко применяется именно несмещенная
статистика
.
Можно показать, что основанная на выборке
объема n выборочная
дисперсия несмещенной оценки
параметра
равна
.
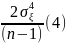Альтернативными выборочной дисперсии, оценками рассеяния величины являются выборочные стандартное отклонение и размах.
Определение: Стандартным отклонением S выборки называется квадратный корень из выборочной дисперсии .
Определение:
Размахом выборки
называется разность ее максимального
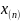и минимального
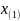значений.
10. Оценивание статистики линейной взаимосвязи двух случайных величин.
Пусть
случайные величины ξ и η представлены
выборкам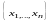и
и
Основной
статистикой – мерой линейной статистической
взаимосвязи двух случайных величин
ξ и η, является выборочный коэффициент
корреляции
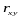
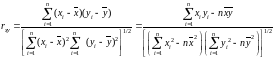
Пример. Изучим линейную статистическую взаимосвязь между ростом (x) и весом (y) 25 произвольно отобранных студентов. Есть выборочные данные:
Предварительно
вычислим вспомогательные суммы:
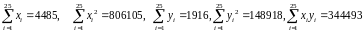
В результате получим:
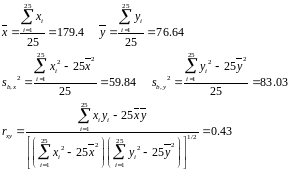
Оценка с выборочного коэффициента корреляции явно не близка к 0, что позволяет считать корреляцию между ростом и весом значимой
11.
Нормальное распределение Гаусса-Лапласа.
В
ряду наиболее известных теоретических
функций распределения важнейшее
прикладное значение имеет функция
нормального или гауссова распределения.
Плотность вероятности и функции
распределения гауссовой случайной
величины ξ с параметрам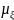и
и
,
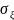имеет вид :Функция плотности вероятности:
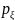(x)=
,
Функция
распределения:
.
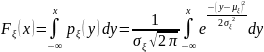Однако
в приложении вместо гауссовой случайной
величины ξ лучше пользоваться стандартной
нормальной величиной ς, принимающей
значения z: z=
,
z
N
,
и имеющей так называемые стандартные
плотность и функцию распределения
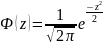
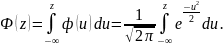
Плотность вероятности ф(z) унимодальная и симметричная относительно моды(точки максимума ф(z)).
Обозначим
через
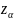значение z, соответствующее
вероятности ф(z) = 1-α, имеем
:
Ф(
)=
=1-α
или
1-Ф(
)=
=
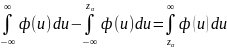P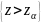
=
α.
Значение
,
удовлетворяющее уравнениям выше,
называется верхней 100α – процентной
точкой или процентилем нормального
распределения.
Процентили
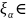N
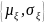и
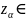N {0,1} нормальных распределений
связаны равенством
=
+
.
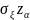Заметим, что ввиду симметричности
функции Ф(z) для α>0,5 имеем
= -
,
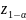а для
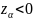нужно использовать соотношение
Ф(
)=1-Ф(-
)
