
- •Случайная величина. Функция распределения в дискретном и непрерывном случае, ее связь с функцией плотности вероятности и ее свойства.
- •Нормально распределенная случайная величина. Как изменяется кривая плотности нормального распределения при изменении его параметров? Что такое стандартное нормальное распределение?
- •3. Определения математической статистики. Типичные задачи матстатистики и их особенности.
- •4 . Выборочный метод. Генеральная совокупность и выборка. Репрезентативная выборка
- •5. Выборочное и теоретическое распределение. Теорема Гливенко. Ее практическая ценность
- •7. Что такое статистика? Качественные свойства статистик.
- •Как вычислить по выборке среднее, медиану и моду?
- •9. Как вычислить по выборке дисперсию, стандартное отклонение и размах.
- •10. Оценивание статистики линейной взаимосвязи двух случайных величин.
- •12. Распределения Пирсона, Стьюдента и Фишера
- •13. Выборочная функция распределения.
- •14. Распределение выборочного среднего при известной дисперсии (известной выборочной дисперсии)
- •15. Распределение выборочной дисперсии.
- •16. Что такое доверительный интервал, доверительные пределы?
- •17. Концепция проверки статистических гипотез
- •19. Критерий согласия «хи-квадрат». Его назначение. Статистика к. Пирсона. Критерий (неравенство) и его интерпретация.
- •20. Полиномиальная регрессия
- •21. Множественная регрессия
- •1.Оценивание параметров модели
- •2.Проверка адекватности модели
- •3.Проверка значимости оценок параметров
Случайная величина. Функция распределения в дискретном и непрерывном случае, ее связь с функцией плотности вероятности и ее свойства.
Действительная функция ξ = ξ(ω), определенная в борелевском поле вероятностей {Ω,F,P} является случайной величиной. Случайная величина
ξ и случайное событие А могут быть связаны соотношением
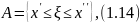
означающим попадание случайной величины
в ξ ∈
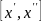 .
Далее будем
.
Далее будем
решать события, оперирующие с конечными, дискретными или непрерывными
случайными величинами ξ , для каждых(k-x) достоверно событие
{−∞ < ξ < +∞} (1.15)
Случайная
величина ξ является дискретной , если
события {ξ = }, k = 1, 2, ... образуют в
}, k = 1, 2, ... образуют в
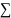 достоверное событие так, что для
вероятностей
достоверное событие так, что для
вероятностей
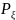 (x)=
P{ξ = x},
(x)=
P{ξ = x},
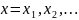 имеем
:
имеем
:

∇
Случайная величина ξ := непрерывной
,если для
 любых
любых
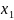 ≤
≤
вероятность
P{
≤ ξ ≤
}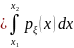 ,
где плотность вероятности
,
где плотность вероятности
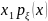 является матрица тельной интегрируемой
функцией , причем :
является матрица тельной интегрируемой
функцией , причем :
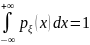
Подчеркиваем, что для случайной величины ξ ∈ вероятность

Функция распределения и ее свойства
P/м дискретную случайную величину ξ ,принимающую одно из значений
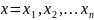 с вероятностью ≠ 0 или ≠ 1. Пусть в опыте
ξ примет
с вероятностью ≠ 0 или ≠ 1. Пусть в опыте
ξ примет
некоторые
из значений
 ,
т.е произойдет событие ,представленное
на-
,
т.е произойдет событие ,представленное
на-
бором
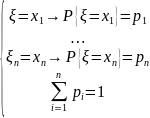
Тогда совокупность вероятностей
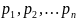 можно трактовать как распределение
суммарной вероятности = 1 между отдельными
значениями случайной величины ξ.
можно трактовать как распределение
суммарной вероятности = 1 между отдельными
значениями случайной величины ξ.
Вероятность того, что случайная величина ξ примет значение меньшее
произвольного действительного числа x , функцией распределения
случайной величины ξ и обозначается:
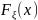 =
P {ξ < x}; −∞ < x < +∞
=
P {ξ < x}; −∞ < x < +∞
Для дискретной случайной величины ξ функция распределения имеет
"ступенчатый"характер:
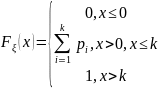
Для непрерывной случайной величины ξ, при существовании плотности
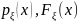 =
=
=
=
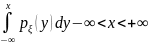 и в каждой своей
и в каждой своей
точке
непрерывности функция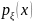 совпадает с производной
совпадает с производной
Свойства:
Функция распределения имеет следующие свойства:
1.Является
монотонно неубывающей , непрерывной
слева функцией
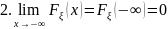
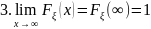
Нормально распределенная случайная величина. Как изменяется кривая плотности нормального распределения при изменении его параметров? Что такое стандартное нормальное распределение?
Непрерывная
случайная величина
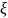 имеет нормальное распределение , если
ее плотность распределения имеет вид:
имеет нормальное распределение , если
ее плотность распределения имеет вид:
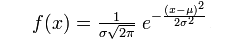
Параметр
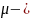 математическое
ожидание. (среднее значение случайной
величины, указывает координату максимума
кривой плотности распределения)
математическое
ожидание. (среднее значение случайной
величины, указывает координату максимума
кривой плотности распределения)
Параметр
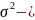 дисперсия,
дисперсия,
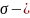 стандартное
отклонение.
стандартное
отклонение.
Нормальное распределение зависит от двух параметров — смещения и масштаба. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Обозначается
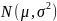
Стандартная
нормальная величина
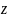 :
:

Где
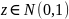
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Стандартные плотность и функция распределения:

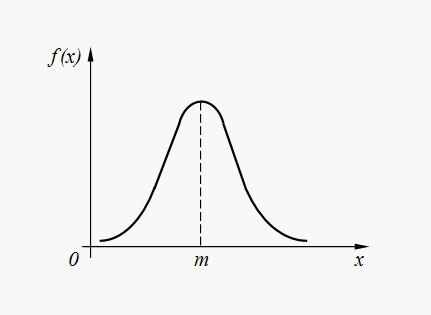
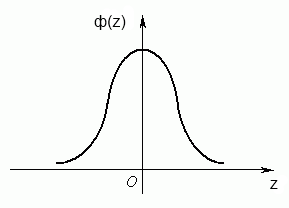
рис(1) рис(2)
(нормальное распределение) (стандартное нормальное распределение)
При изменении мат.ожидания кривая перемещается относительно оси Ox, сохраняя форму.
При изменении стандартного отклонения изменяется форма кривой: утолщаются хвосты, колокол становится ниже.
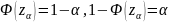
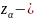 верхняя
верхняя
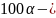 процентная
точка (процентиль) нормального
распределения.
процентная
точка (процентиль) нормального
распределения.
