Уравнение состояния идеальных газов.
Уравнение, выражающее связь между параметрами равновесного состояния термодинамической системы идеального газа.
Уравнение состояния идеального газа впервые было получено Клапейроном путем объединения уравнений законов Бойля-Мариотта и Гей-Люссака pν/T=const. Обозначая константу через R, получим уравнение для 1 кг газа.
Pν = RT, |
(1) |
где R –удельная газовая постоянная, отнесенная к массе газа, Дж/кг·К.
P- абсолютное давление, Па=Н/м2,
T – абсолютная температура газа. К,
ν - удельный объем газа,м3/кг
Учитывая, что плотность газа ρ = 1/ ν перепишем уравнение (1)
Р = ρ RT |
(2) |
где ρ – плотность газа, кг/м3.
Умножая обе части уравнения (1) на массу газа м, получим уравнение состояния для м кг газа, где м не равно 1.
РV = m RT (m≠1) (3)
где – Р- абсолютное давление, Па=Н/м2,
V – объем м кг газа, м3,
m – масса газа, кг,
R –удельная газовая постоянная, отнесенная к массе газа, Дж/кг·К
T – абсолютная температура газа. К
Умножая обе части уравнения (1) на молярную массу газа μ, получим уравнение состояния для 1 кмоля газа
Рνμ = μRT или РVμ = μRT (4)
где – Р- абсолютное давление, Па=Н/м2,
Vμ – объем 1 кмоля газа, м3/кмоль,
μ – молярная масса газа, кг/кмоль,
R –удельная газовая постоянная, отнесенная к массе газа, Дж/кг·К,
T – абсолютная температура газа, К.
μR- универсальная газовая постоянная, Дж/кмоль·К.
Выведем значение, размерность и физический смысл μR .
Из ур-ия (4) вычислим μR при нормальных физических условиях (Т0=273К, Р0=101332Па и
Vμ =22,4 м3/кмоль
μR
=
(5)
Учитывая (5) перепишем (4)
РVμ = 8314T (6)
Это ур-ие носит название Клапейрона-Менделеева.
Универсальная газовая постоянная имеет одинаковое значение для 1кмоля любого газа, в том числе смеси и равна 8314Дж/кмоль·К.
[μR]=
удельная газовая постоянна для данного газа и зависит от молярной массы газа.
=
[R]=8314/μ=Дж·кмоль/кмоль·К·кг=Дж/кг·К.
Смеси газов.
а)
- для 1 кмоля смеси газов.
(7)
(8)
(9)
;
=
;
(10)
(11).
Параметры смеси вычисляются по правилу аддитивности.
,
(12)
где
R
R
R
-удельная
газовая постоянная компонентов смеси;
Дж/кг·К.
доля
компонентов смеси, безразмерная величина.
(13)
где
-молярная
масса компонента; кг/кмоль
В термодинамике для газов мольные и объемные доли принимаются одинаковыми. Если параметр отнесен к массе, то берем Х, если к молям(объему)-У
б) для 1 кг смеси газов:
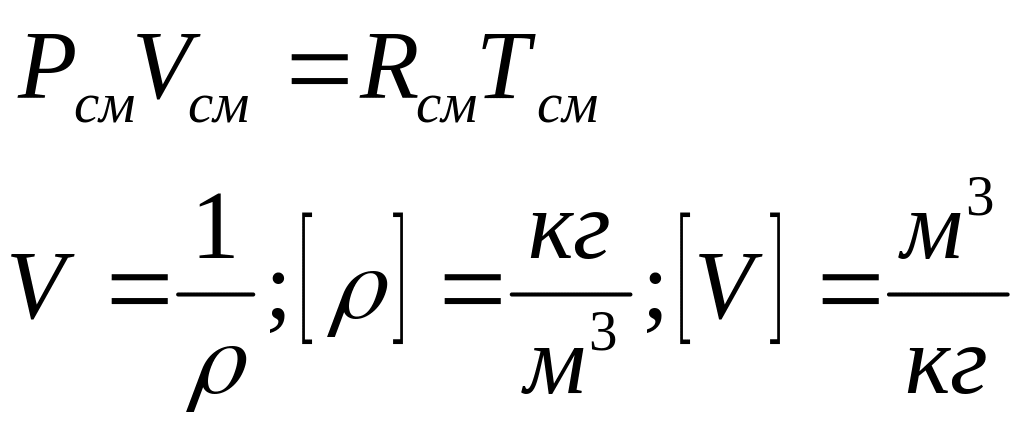(14)
(15).
в) для m кг смеси газов:
(16)
(17)
(18)
yi- мольная доля компонента
хi- массовая доля компонента
i- молярная масса компонента
cм-молярная масса смеси.
Закон Дальтона -1) общее давление = сумме парциальных давлений.
(19)
- 2) парциальное давление пропорционально давлению смеси и мольной (объемной) доле компонента.
(20)