С учетом этого уравнение (8.2) перепишем в виде

+ RI + = . (8.3)

Преобразуем уравнение к виду

или

, (8.4)

где

 коэффициент затухания;

 собственная частота колебательного контура.

Линейное, неоднородное дифференциальное уравнение второго порядка (8.4) называют уравнением колебательного контура.

8.2. Свободные электрические колебания

Если в колебательном контуре активное сопротивление R = 0 и отсутствует внешняя ЭДС ( = 0), (рис. 8.1), то возникающие колебания в контуре называют свободными незатухающими электрическими колебаниями.

Уравнение (8.4) в этом случае принимает более простой вид,

т. е.

. (8.5)

Решением этого линейного, однородного дифференциального уравнения второго порядка является функция

q = q₀ cos(₀t + ₀), (8.6)

где q₀  амплитудное значение заряда на обкладках конденсатора; ₀  собственная частота контура; ₀  начальная фаза.

Значения q₀ и ₀ являются начальными условиями, например, значение заряда q и в момент времени t = 0.

Величина начальной фазы ₀ определяется свойствами контура.

Так как

и ,

то период свободных незатухающих колебаний определяется по формуле Томсона

. (8.7)

Дифференцируя (8.6) по времени найдем уравнение колебания силы тока в контуре

I =  q₀₀ sin(₀t + ₀) (8.8)

или

I = I₀ cos(₀t + ₀ + ),

где I₀ = q₀₀  амплитудное значение силы тока.

Уравнение колебания напряжения на конденсаторе

U = q₀ cos(₀t + ₀), (8.9)

где

 амплитудное значение напряжения.

Вывод: При свободных незатухающих колебаниях напряжение на конденсаторе находится в фазе с зарядом q, а ток I опережает по фазе напряжение U на конденсаторе на .

8.3. Затухающие электрические колебания

Рис. 8.3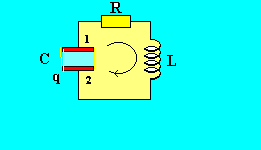

Если внешняя ЭДС отсутствует ( = 0), активное сопротивление R  0 (рис. 8.3), то свободные колебания в контуре будут затухающими, так как часть энергии расходуется на нагревание проводников.

Уравнение свободных затухающих колебаний запишем в виде

. (8.10)

Решением этого линейного, однородного дифференциального уравнения является функция

, (8.11)

где  - круговая частота затухающих колебаний

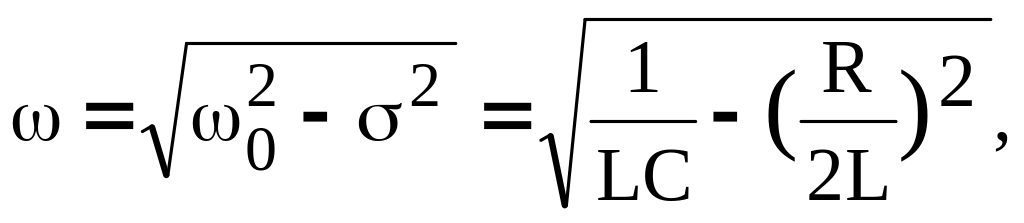(8.12)

q₀ и ₀ - произвольные постоянные, определяемые из начальных условий.

График свободных затухающих колебаний приведен на рис. 7.4.

Произведение в формуле (8.11) называют амплитудой затухающих колебаний.

Период свободных затухающих колебаний определяется формулой

Рис. 8.4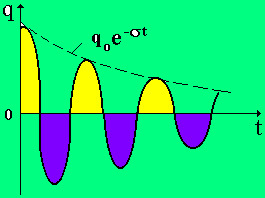

. (8.13)

Зная зависимость q(t), можно найти напряжение на конденсаторе

(7.14)

и ток в колебательном контуре

или

(8.15)

где

Следовательно, ток опережает по фазе напряжение на конденсаторе более чем на , так как угол  находится в интервале ( <  < ).

Графики зависимостей U(t) и I(t) имеют вид, аналогичный графику рис. 8.4, для q(t).

Свободные затухающие колебания характеризуются следующими свойствами:

1. Коэффициент затухания

.

2. Время релаксации

,

где  - время, за которое амплитуда колебаний уменьшается в е раз.

3. Логарифмический декремент затухания . Его определяют как натуральный логарифм отношения двух значений амплитуд, отличающихся на период Т, т. е.

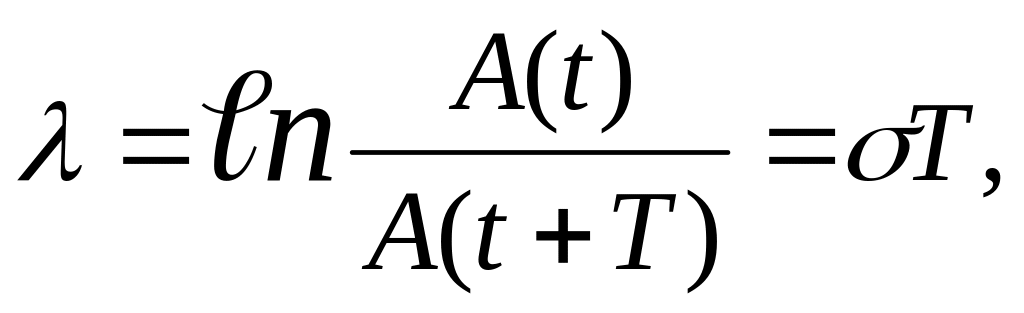(8.16)

где А - амплитуда соответствующей величины q, U или I.

4. Добротность колебательного контура

Q = . (8.17)

В случае слабого затухания

. (8.18)

При ² колебаний не наблюдается, а происходит лишь апериодический разряд конденсатора.