. Застосування інтегрального числення 197

Розділ 10

Застосування інтегрального числення

1. Обчислення площ плоских фігур

2. 1.1 Обчислення площ плоских фігур у декартовій системі координат

Якщо на відрізку задана неперервна функція , то, згідно з геометричною інтерпретацією визначеного інтеграла, площа криволінійної трапеції, обмеженої кривою , прямими , та віссю (рис.1), обчислюється згідно з формулою:

. (1.1)

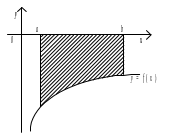
Рис.1 Рис.2

Криволінійні трапеції (рис.1 – при , рис.2 – при )

Якщо на відрізку функція (рис.2), то криволінійна трапеція буде розміщена у нижній півплощині і відповідний визначений інтеграл буде від’ємним. Оскільки площа фігури є величиною невід’ємною, то її можна обчислити згідно з формулою

, . (1.2)

Якщо на відрізку функція декілька разів змінює знак (рис.3), то інтеграл на відрізку слід розбити на суму інтегралів по часткових відрізках – відрізках знакосталості функції. Інтеграл буде додатнім на тих відрізках, на яких та від'ємним там, де . Інтеграл на відрізку дає різницю площ фігур, що лежать вище та нижче осі .

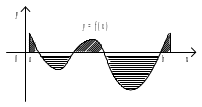
Рис.3 . Геометрична інтерпретація інтеграла від

знакозмінної функції

Щоб знайти суму площ без врахування розташування відносно осі , треба знайти суму абсолютних величин інтегралів на відрізках знакосталості функції або обчислити інтеграл від абсолютної величини функції, тобто (рис.4)

. (1.3)

Рис.4. Геометрична інтерпретація інтеграла

від модуля функції

П риклад 1.1. Обчислити площу фігури, обмеженої лініями та на проміжку .

 Згідно з формулою (1.1) для невід'ємної на функції матимемо

(кв.од.) .

Якщо треба обчислити площу фігури, розміщеної між лініями , та прямими , ( на відрізку ) (рис.5), то формула площі запишеться

. (1.4)

Рис.5.

Приклад 1.2. Обчислити площу фігури, обмеженої параболами ; .

 Розв’язуючи систему рівнянь , знаходимо абсциси точок перетину: ; .

В важаючи , на підставі формули (1.4) отримаємо

(кв.од.).

1.2. Обчислення площ фігур, що обмежені лініями, заданими параметрично.

Якщо необхідно обчислити площу криволінійної трапеції, обмеженої лінією, що задана у параметричній формі

, , (1.5)

де , , , то у формулі перейдемо до нової змінної, беручи за незалежну змінну .

З рівняння (1.5) маємо і

. (1.6)

Це формула для обчислення площі криволінійної трапеції, обмеженої лінією, що задана параметрично.

Приклад 1.3. Обчислити площу еліпса , .

 Площу еліпса будемо обчислювати як подвоєну площу його верхньої половини (див. рис.), для якої змінюється від до , отже параметр набуває значень від до . Враховуючи, що , матимемо

.

(Якщо , то еліпс перетворюється в коло і площа відповідного круга дорівнює ).