Б-1

Мощность мн-ва. Счётность мн-ва рациональных чисел. Несчётность мн-ва дей-х чисел.

Опр-е: Если для мн-в А и В имеет место случай 1), то ; 2) - ; 3) - (где 1) А~В₁, где В₁ В, но В не экв. никакому подмн-ву мн-ва А; 2) В~А₁, где А₁ А, но А не экв. никакому подмн-ву мн-ва В; 3) А~В₁, где В₁ В и В~А₁, где А₁ А)

Опр. распр-ся на конечные и ∞ мн-ва

Опр-е. Всякое мн-во, ~-ное мн-ву N, наз-ся счётным.

Опр-е. Мн-во наз-ся счётным, если его элементы можно пронумеровать натур. индексами, т. е. расположить в виде ∞-ной -сти m₁, m₂, …,m_n,…

Мощность счётного мн-ва называется счётной мощностью и обозначается через a.

Теорема 1. ∞-ное мн-во точек с натур-ми координатами пространства счётно.

Теорема 2.Объединение счётного мн-ва счетных мн-в есть счётное мн-во.

Теорема 3.Мн-во всех рац-ых чисел счётно.

Доказательство. Всякое рац-ое число представляется в виде p/q, где p,q . Рассмотрим «+»-ые дроби p/q, где p,q . Мн-во таких дробей ~-но мн-ву элементов вида a_p,q с натур. индексами, которое счётно. Мн-во Q всех рац. чисел как сумма «+»-ных и «-»-ных дробей и числа 0 счетно как объединение конечного и счётного мн-ва. Ч.Т.Д.

Теорема 4. Мн-тво действ-ых чисел х, удовл-ющих неравенствам 0х1 несчетно.

Доказательство. Пусть мн-во точек сегмента [0,1] счетно. Тогда все эти точки (числа) можно расположить в виде -сти x₁, x₂,…, x_n,… (1)

Разделим [0,1] = Δ на 3 =ые части точками 1/3 и 2/3. Выберем из них ту часть, которая не x₁ . Обозначим ее через Δ₁ и снова разделим на 3 =ые части и обозначим через Δ₂ ту, которая не х₂.

Продолжая этот процесс неограниченно, получим -сть вложенных сегментов Δ Δ₁ … Δ_n …, причем Δ_n не х_n, . Длина Δ_n = 1/3ⁿ и при . По принципу вложенных сегментов точка С , -ая всем сегментам {Δ_n}.Точка С принадлежит и [0,1].

С другой стороны, точка С не может в (1), т.к. если бы она в ней, то по построению {Δ_n} она не входила бы хотя бы в один из сегментов Δ_n. Противоречие.

Опр-е. Мн-во, ~-ное мн-ву действ-ных чисел, -щих [0,1], наз-ся мн-вом мощности континуума. Мощность континуума обозначают через С.

Теорема 5. Всякий сегмент, интервал, полуинтервал яв-ся мн-вом мощности континуума.

Док-во: Достаточно показать, что сегмент [a;b] ~[0;1], т.к. удаление 1 или 2 точек не меняет мощности мн-ва. Пусть y [a;b], х [0,1], тогда ф-ция y=(b-a)x+a устанавливает взаимно однозначное соот-вие м/у [a;b] и [0;1].

Б-2

Предел и непрерывность функций в точке. Св-ва непрерывных функций на отрезке.

Опр-е. Точка x наз-ся предельной точкой мн-ва М, если в окрестности точки х хотя бы одна точка мн-ва М, отличная от х.

Пусть ф-ция у = f(x) определена на интервале (а,b) всюду, кроме, быть может, точки х_о (а,b). Ясно, что точка х_о - предельная точка для (а,b).

Опр-е. Число А наз-ся пределом ф-ции f(x) в точке х_о, если для {х_n} такой, что х_n (а,b), вып-ся условие

Если такое число А существует, то говорят, что функция y=f(x) имеет предел в точке х_о и пишут или при .

Опр-е (по Коши). Число А наз-ся пределом ф-ции f(x) в точке х₀ , если для всякого наперед заданного как угодно малого >0 такое число >0, зависящая только от  и такое что ,удов-щих условиям вып-ся неравенство .

Опр-е. Функция f(x), определенная на (а,b),наз-ся непрерывной в точке х₀ (а,b), если предел ф-ции в точке х₀ равен значению ф-ции в этой точке, т.е. .

Теорема. (Вейерштрасса). Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значение.

Док-во. Пусть f(x) непрерывна на [а,b], тогда он ограничена на [а,b]. Т.е. мн-во значений ф-ции ограничено сверху. Пусть , где M-const. Покажем, что такое, что f(x₁)=M.

Допустим противное, т.е. , .

Рассмотрим ф-цию . Она непрерывна на [a;b] (нет деления на 0) и следовательно ограничена на [a;b].

По опред. верх. грани для , такое что , тогда . Отсюда видим, что за счет выбора м/б сделана как угодно большой, т.е. не ограничена на [a;b]. Противоречие. Значит сущ-ет хотя бы 1 точка ,в которой f(x₁)=M.

Пусть , тогда т.к. f(x) – непрерывна на [a;b], то , такое что –f(x₂)=-m, т.е. f(x₂)=m. ЧТД

Б-3

Предел числовой последовательности. Теорема Больцано-Вейерштрасса.

Опр-е. Число А наз-ся пределом послед-сти {х_n}, если номер N, зависящий только от ε, такой, что для всех n > N ,удовлетворяют нер-ву . Пишут .

Число N зависит только от и потому пишут N ( ) или . Нер-во равносильно А- <х_n<А+ . Значит, если А -предел послед-сти {х_n}, то все ее члены с номерами n > N лежат -окрестности точки А. Члены с номерами n N могут находиться где угодно, но начиная с Х_N+1 все они находятся в (А- ,А+ ). Так, что вне этого интервала наход-ся только конечное число членов.

Послед-ость, имеющая предел, наз-ся сходящейся. {}-сть, не явл-ся сходящейся, наз-ся расходящейся.

Теорема (Больцано - Вейерштрасса). Из любой ограниченной {}-сти можно выделить сходящуюся под{}-сть.

Доказательство. Пусть {х_n}ограничена т.е. .

Разделим [а,b] пополам. По крайне мере одна из половин содержит ∞-ное мн-во элементов из {х_n}. Эту половину обозначим через [а₁,b₁]. Пусть - какой - нибудь член {}-сти, лежащий в [а₁,b₁]. Разделим [а₁,b₁] опять пополам, Снова хотя бы одна из половин содержит ∞-ное мн-во членов из {х_n}. Обозначим ее через [а₂,b₂]. Выберем точку и т.д.

Получим {}-сть сегментов [а_к,b_к] и {}-сть точек {}-сти {х_n}, к=1,2,... {}-сть пo построению является подпослед-стью {}-сти {х_n}.

Сегменты [а_к,b_к] (к=1,2,...) образуют систему влож-х отрезков, причем . По принципу влож-х отрезков существует единственная точка с, принадлежащая всем отрезкам, , . По построению, . По теореме о пределе промежуточной переменной .ЧТД

Теорему можно сформулировать иначе: всякая ограниченная {}-сть имеет по крайне мере 1 частичный lim.

Б-4

Определение и существование степени с иррациональным показателем.

Сначала докажем некот. св-ва степени с рац-ым показателем , r-рац-ное число.

Лемма1. Если а>1, то

Лемма2. Если а>1 и - рац-ные числа, то .

Лемма3.

Лемма4. Пусть - произвольная {}-сть рац-х чисел, сходящаяся к 0; а>1 – любое действ-ное число. Тогда .

Пусть - произвольное иррац-ное число. Всякое иррац-ное число яв-ся пределом некоторой {}-сти рац-х чисел .

Лемма5. Если а>0, -иррац-ое число, то для всякой {}-сти рац-х чисел , сходящейся к , . сх-ся к одному и тому же пределу.

Док-во. 1). Пусть а>1. Сначала возьмём неубывающую {}-сть рац. чисел .

По лемме 2 Т.к. сх-ся, то она ограничена сверху. Пусть . Снова по лемме 2 , т.е. ограничена сверху и потому она имеет предел .

Пусть теперь {}-сть рац-х чисел произвольна и .Рассмотрим .Т.к. , то по лемме 4 . Тогда , т.е. .

2). Если 0<a<1, то . Только что показано, что любая послед-сть , где имеет один и тот же предел: . Тогда . Лемма доказана.

Опр-е. За значение степени с иррац-м показателем принимает предел, к которому сходится {}-сть , где - любая {}-сть рац-х чисел, сходящаяся к .

Степень с иррац-ным показателем обладает свойствами:

; . Действительно, пусть . Тогда .

Б-5

Степенная функция с иррациональным показателем. Степень в комплексной области.

Рассмотрим степенную ф-цию у = , где - иррац-ное число.

Т.к. здесь допустимы лишь x>0, то можно записать .

Ф-ция у = яв-ся сложной, где .

Свойства:

1.

2. Монотонно возрастает в D(у) при >0 и убывает при <0.

Доказательство. Пусть α>0 => и . Т.е. => =>y₁<y₂ - монотонно возрастает. При <0 аналогично (монотонно убывает).

3. Непрерывна в D(f) по теореме о непрерывности сложной функции.

4.

Доказательство. Пусть >0, тогда при , ; . При <0 ; .

5.

Доказательство. Пусть >0 , , . Если <0 .

Степень в комплексной области.

Пусть а≠0 – произвольное комп. число. При целом n , . Получаем одно значение степени.

Пусть r=p/q – несокр.дробь, т.е. r – рацион. число.

Имеем , k=0, 1,…,q-1

Имеем q значений степени. Запишем иначе:

для примера:

Для произвольных комплексных а и α по определению полагают: (1) – формула универсальна.

Степень с произв. показателем не подчиняется известным законам умножения и возведения в степень

,

6. Сущ-е лог-ов. Лог-ая ф-ия. Лог-м в компл-ой области

Опр. 1. Логарифмом числа b по основанию а (а > 0, a ≠ 1) наз-ся показатель степени, в которую нужно возвести а, чтобы получить b. Пишут .

- основное логар-ое тождество (1)

Возведем его обе части в степень . . Отсюда

(2)

Т. 1. Для  дейст-го числа b > 0   логарифм при  основании а > 0, a ≠ 1.

Д. Пусть а > 0, b > 0. Рассм-м ф-цию y=a^x. Т. к. , , то, по теореме о промежуточном значении непрерывной ф-ции, ф-ция у = а^х принимает  «+»-ное значение. В силу монотонности ф-ции  значение принимается один раз. След-но, для любого b   число х, такое что , где x=log_ab.

Случай 0 < a < 1 аналогичен. .

Пусть теперь с > 0, с ≠ 1. согласно (1). Прологарифмируем по основанию а. согласно (2). Отсюда (3). Положив в (3) х = а, находим .

Рассм-м y = f(x) = log_ax ( a > 0, a  1). Она обратна по отношению к функции у = а^х.

1. D(y) = (0, +).

2. log_a1 = 0, log_aa = 1

3. Если а >1, то если 0 <a <1, то

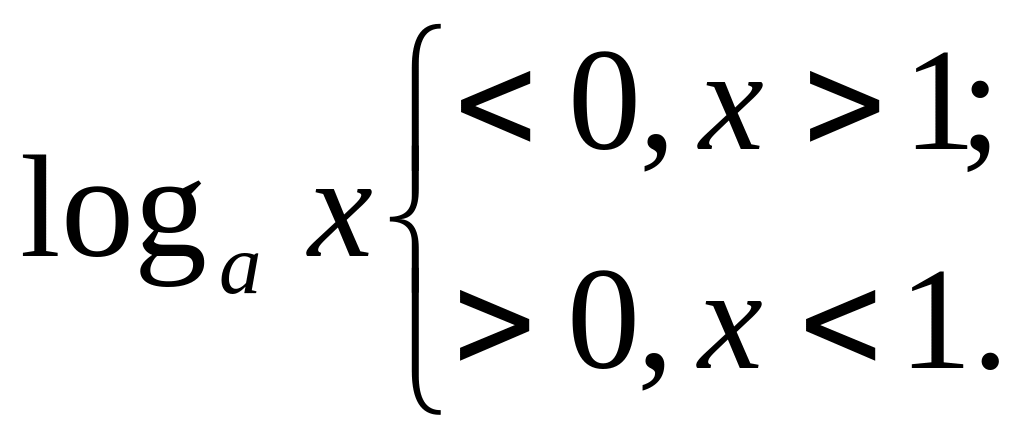
Д. Пусть а > 1. Тогда . Получили доказуемое, только в другом порядке. Случай 0 < a < 1 аналогичен.

4. y = log_ax непрерывна в D(y) как обратная к непрерывной и монотонной функции y = а^x.

5. При а > 1 монотонно возрастает на ( 0, +); при 0 < a < 1 монотонно убывает как обратная функция к y = а^x.

6. 

Д. Пусть а > 1. В равенстве при х+ будет log_ax+ согласно свойству функции y = а^x. При 0 < a < 1 отсюда же log_ax- .

7. 

Д. Пусть а > 1. В при х+0 будет log_ax-. При 0 < a < 1 отсюда же log_ax+ .

8. , (х₁ > 0, x₂ > 0).

Д. , . и далее по определению логарифма.

9. , (х₁ > 0, x₂ > 0).

10. , (х > 0,   R).

Число w называется логарифмом числа z, если expw = z. Пишут w = Lnz.

Св-ва логарифмов:

1. , (z₁ ≠ 0, z₂ ≠ 0)

2. , (z₁ ≠ 0, z₂ ≠ 0)

3. , ( z_k ≠ 0, k)

4. 

Для главных значений логарифмов (ln) не вып-ся даже св-ва 1 и 2, т. к. мнимая часть левой и правой частей должна лежать в (-π, π].