Определение случайного вектора

Пусть

основное вероятностное пространство

пространство векторов с борелевской сигма-алгеброй

поточечное измеримое отображение, ставящее в соответствие каждому элементарному исходу основного пространства действительный вектор. Это отображение называется случайный вектор.

Вероятностная мера, определенная на борелевской сигма-алгебре по формуле

называется распределением случайного вектора.

Пусть

случайный вектор и

Функция

называется функция распределения (иначе - совместная функция распределения) случайного вектора

Аналогично одномерному случаю определяются дискретные и непрерывные случайные вектора и их распределения.

Плотность распределения случайного вектора f(x) – это функция, удовлетворяющая условию

Мера Лебега в конечномерном пространстве

Мера Лебега в конечномерном пространстве это мера, приписывающая параллелепипеду его объем. В частности, мера Лебега прямоугольника это его площадь.

Мера Лебега на квадрате - Задача о встрече

Рассмотрим следующую задачу.

Два человека договорились встретиться в определенном месте в течение часа и ждать друг друга не более 10 минут. Найти вероятность, того они встретятся, если момент прихода каждого совершенно случаен.

Для решения задачи построим следующую вероятностную модель. Исходом опыта является вектор

где первая координата – момент прихода первого человека, вторая – момент прихода второго. Сигма-алгебра – все борелевские подмножества единичного (1 час=1 единица времени) квадрата. Предположение о совершенной случайности моментов прихода приводит к вероятностной мере, которая приписывает каждому множеству единичного квадрата его площадь. Эта мера называется мера Лебега на квадрате. Подсчитаем вероятность интересующего нас события. Два человека встретятся, если

Площадь этой наклонной полосы

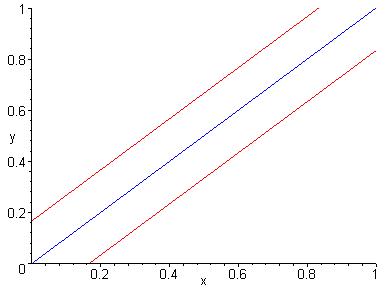
равна

Независимые случайные величины

Случайные величины

,

заданные на одном вероятностном пространстве, называются независимыми, если для любых борелевских множеств

Можно показать, что независимость случайных величин эквивалентна тому, что их совместная функция распределения равна произведению их одномерных функций распределения

Если случайные величины независимы и имеют совместную плотность, то она является произведением их одномерных плотностей. Верно и обратное.

Многомерное нормальное распределение

Пусть

вектора

- симметричная положительно определенная матрица размера k x k,

матрица , обратная к

- транспонированная матрица,

- определитель матрицы A.

Распределение с плотностью

называется многомерным нормальным распределением с параметрами

Многомерное нормальное (гауссовское распределение) является обобщением одномерного нормального распределения и обычно используется для моделирования опытов, в которых одновременно имеются несколько одномерных нормальных величин, связанных между собой.

Если матрица диагональная, то случайные координаты многомерного нормального случайного вектора независимы.

В важном частном случае (k=2) многомерное нормальное распределение превращается в двумерное. Матрица

где диагональные элементы положительны,

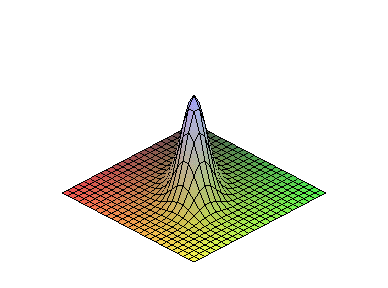
положительно определена и плотность имеет вид

Смысл параметров

и , в общем случае элементов матрицы

будет объяснен в дальнейшем. График плотности при

приведен ниже