
- •1. Опыт: бросание монеты 13
- •2. Опыт: бросание игральной кости 14
- •Возникновение и развитие теории вероятностей До появления аксиоматики Колмогорова
- •В наше время
- •Необходимость теории вероятностей как науки
- •Возможность анализа случайных явлений
- •Новый язык для описания объектов
- •Распространение вероятностной и статистической терминологии
- •Элементарный исход
- •1. Опыт: бросание монеты
- •2. Опыт: бросание игральной кости
- •Пространство элементарных исходов
- •Советы по построению пространства элементарных исходов.
- •Определения Подмножества
- •Алгебра и сигма-алгебра
- •Вероятностное пространство
- •Парадокс определения вероятностного пространства
- •Дискретная вероятностная модель
- •Конечное пространство элементарных исходов
- •Классическая вероятностная модель
- •Связь классической вероятностной модели с комбинаторикой
- •Основная формула комбинаторики
- •Урновая схема
- •Общее определение вероятности для экспериментов с конечным или счетным числом исходов
- •Дискретное распределение и вероятность
- •Равномерное распределение - классическая вероятностная модель
- •Биномиальное распределение – схема Бернулли
- •Мультиномиальное распределение – схема бросания частиц по ячейкам
- •Геометрическое распределение – испытания до первого успеха
- •Распределение Паскаля – испытания до m-того успеха
- •Пуассоновское распределение - теорема Пуассона
- •Теорема Пуассона.
- •Независимость событий и условная вероятность. Построение моделей.
- •Независимость Различие между независимостью попарно и в совокупности. Пример Бернштейна
- •Использование понятия независимости для построения моделей. Произведение вероятностных пространств.
- •Примеры построения моделей.
- •Расчет надежности при параллельном соединении элементов.
- •Расчет надежности при последовательном соединении элементов
- •Расчет надежности сложной системы.
- •Замечания к примерам.
- •Условная вероятность
- •Урновая схема
- •Марковская зависимость
- •Формула полной вероятности и формула Байеса
- •Случайные величины
- •Отображения вероятностных пространств
- •Случайная величина
- •Борелевская сигма-алгебра
- •Определение случайной величины
- •Распределения случайных величин и векторов Функция распределения
- •Дискретные распределения на прямой
- •Вырожденное распределение
- •Бернуллиевское распределение
- •Биномиальное распределение
- •Геометрическое распределение
- •Пуассоновское распределение
- •Произвольное дискретное распределение
- •Функция распределения случайной величины
- •Непрерывные распределения на прямой
- •Равномерное распределение на отрезке.
- •Мера Лебега на прямой.
- •Плотность распределения
- •Вероятностный смысл плотности распределения
- •Бета-распределение на отрезке [0,1]
- •Смеси распределений.
- •Нормальное (гауссовское) распределение.
- •Экспоненциальное (показательное) распределение.
- •Гамма-распределение.
- •Построение меры в конечномерном пространстве Борелевская сигма-алгебра в конечномерном пространстве
- •Определение случайного вектора
- •Мера Лебега в конечномерном пространстве
- •Мера Лебега на квадрате - Задача о встрече
- •Независимые случайные величины
- •Многомерное нормальное распределение
- •Числовые характеристики случайных величин и векторов
- •Интеграл Лебега – математическое ожидание
- •Свойства интеграла Лебега (математического ожидания)
- •Неравенства Неравенство Маркова
- •Неравенство Чебышева. Дисперсия
- •Неравенство Коши-Буняковского-Шварца. Ковариация
- •Неравенство Йенсена.Выпуклые функции
- •Моменты
- •Вычисление математического ожидания.
- •Теорема Лебега о замене переменных
- •Вычисление интеграла Лебега на прямой.
- •Вычисление маргинальных плотностей
- •Вычисление числовых характеристик важных распределений.
- •Взаимосвязь различных видов сходимости
- •Закон больших чисел в форме Бернулли
- •Предельные теоремы теории вероятностей
- •Закон больших чисел в форме Чебышева
- •Определение условного распределения и условной плотности Условное распределение
Функция распределения случайной величины
Если случайная величина имеет распределение с функцией распределения F, то говорят, что F – функция распределения случайной величины. В этом случае, очевидно,
![]()
Если нам будет важно отметить, какой случайной величине соответствует функция распределения F, будем отмечать это так
![]()
Непрерывные распределения на прямой
Распределение называется непрерывным, если его функция распределения непрерывна. Случайная величина, имеющая непрерывное распределение, обычно называется непрерывная случайная величина.
Для дискретных распределений мы вычисляли функцию распределения, зная вероятность. Теперь, наоборот, мы будем задавать функцию распределения и исследовать свойства получающейся вероятности.
Равномерное распределение на отрезке.
Рассмотрим следующую функцию распределения


Какими свойствами обладает вероятность, соответствующая этой функции распределения?
Нетрудно увидеть, что вероятность отрезка, целиком лежащего внутри отрезка [0,1], равна его длине.
![]()
В общем случае для любого отрезка
его вероятность равна длине его пересечения с отрезком [0,1]
![]()
Вероятность одноточечного множества равна нулю.
Такая вероятностная мера называется мера Лебега на отрезке [0,1] или равномерное распределение на отрезке [0,1].
Равномерное распределение применяется в тех случаях, когда исход опыта – абсолютно случайная точка отрезка [0,1], например, случайный момент времени. Во многих языках программирования есть функция, возвращающая случайное число из отрезка [0,1] (rand(), random() и т.п. ) – датчик случайных чисел. Используя равномерное распределение, можно моделировать другие распределения, например, бернуллиевское. Действительно, если
![]()
равномерно распределена на отрезке [0,1], то
случайная величина
![]()
имеет
бернуллиевское распределение с параметром p.
Рассмотрим следующую функцию распределения

Покажите, что если
|
эта функция распределения называется функция распределения равномерного распределения на отрезке [a,b]. Случайная величина, имеющая равномерное распределение на отрезке [a,b], называется равномерно распределенная на отрезке [a,b] случайная величина. Для равномерного распределения используют обозначение
|
Мера Лебега на прямой.
Можно показать, что существует (не вероятностная) мера на прямой, которая приписывает каждому отрезку его длину. Эта мера называется мера Лебега (на прямой). В дальнейшем будем обозначать эту меру
Плотность распределения
В тех случаях, когда функцию распределения можно представить в виде интеграла (Римана) от неотрицательной функции
![]()
функцию f называют плотностью, соответствующей функции распределения F, или плотностью F .
Если функция распределения имеет плотность, то эта функция распределения непрерывна и такие функции распределения называют абсолютно непрерывными.. Заметим, что представление функции распределения в виде интеграла от некоторой функции неоднозначно, поэтому у одной функции распределения может быть несколько различных плотностей. Впрочем, различаться они могут только в не очень большом числе точек. Поэтому обычно плотностью называют наиболее прилично ведущую себя функцию f – непрерывную или почти непрерывную. Ее и приводят в различных справочниках. Нарисуем, например, график плотности равномерного на отрезке [0,2] распределения.

Очевидно, любая плотность удовлетворяет условию
![]()
Зная плотность распределения нетрудно подсчитывать вероятности различных множеств.

и, вообще, если индикаторная функция
![]()
множества
![]()
интегрируема по Риману на любом конечном отрезке, то
![]()
Если g(x) – неотрицательная функция, удовлетворяющая условию
![]()
то функция

будет функцией распределения с плотностью
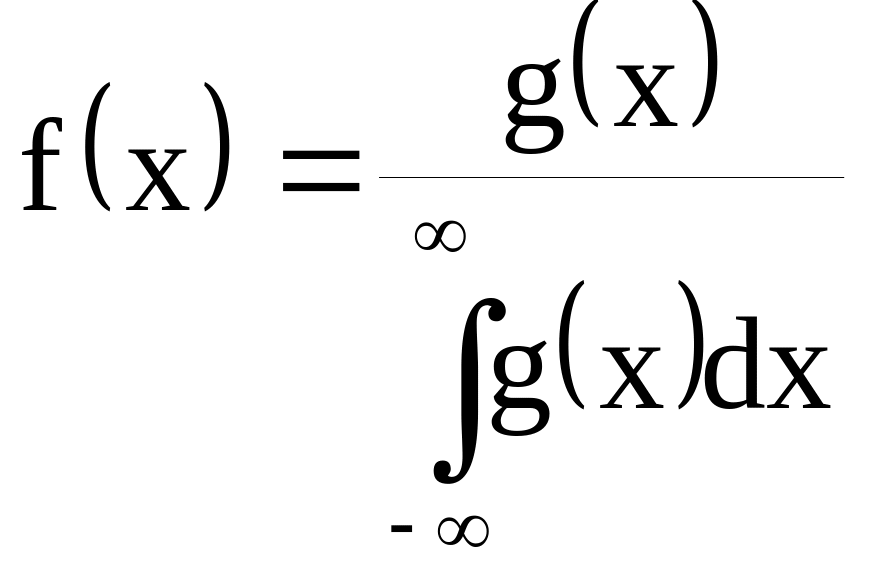
Этот факт позволяет построить множество примеров непрерывных функций распределения
