5 Расчет переходных процессов операторным методом

Исходные данные:

Е = 125 В

R₁= 50 Ом

R₂= 200 Ом

R₄= 250 Ом

L = 0,01 Гн

С = 5 мкФ

Определить ток i_L в переходном режиме.

Для составления эквивалентной операторной схемы определим независимые начальные условия i_L(0) и u_C(0) по законам коммутации:

i_L(0) = i_L(0_-) = = 0,25 А; u_C(0) = u_C(0-) = = 50 В.

Составим эквивалентную операторную схему:

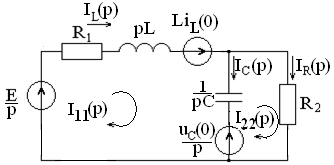
Рисунок 5.2

Составим уравнения методом контурных токов относительно изображений контурных токов по схеме рисунок 5.2.

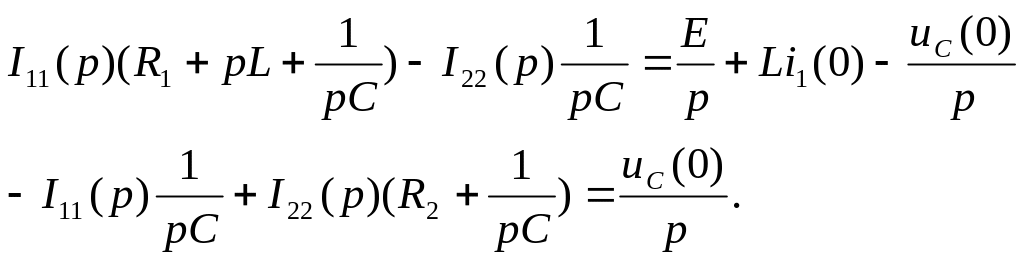
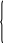(5.1)

В среде MathCad решить систему уравнений (5.1) можно различными способами.

Способ 1. Набрать систему уравнений в шаблоне матрицы, с числом строк - 2 и числом столбцов - 1. Между левой и правой частями уравнений поставить логический знак равенства. Применить к системе уравнений, записанных в виде матрицы, операторы «solve», «explicit», «collect» которые находятся на панели «Символика» и используются для решения системы уравнений в символьном виде относительно заданной переменной.

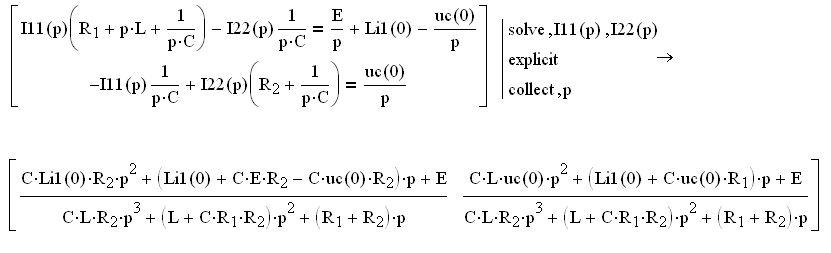
Способ 2. Решить систему уравнений в матричной форме путем обращения матрицы коэффициентов. Где Z – квадратная матрица контурных сопротивлений; E_k – матрица-столбец контурных ЭДС; I_кк (p) – матрица-столбец контурных токов.

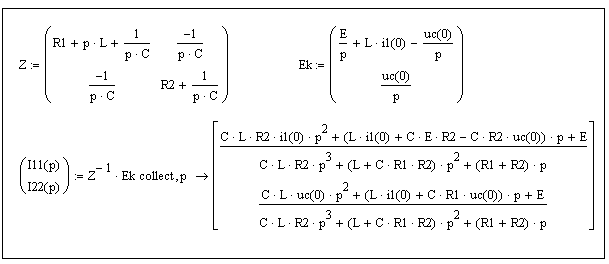
Таким образом:

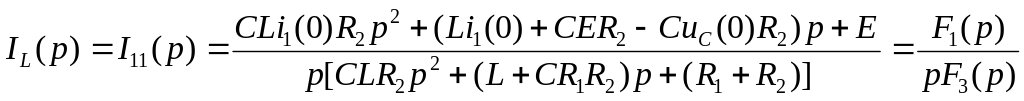
. (5.2)

Для определения корней характеристического уравнения приравняем знаменатель выражения (5.2) к нулю.

Следовательно один корень р=0, остальные корни определяются из выражения

(5.3)

Решение квадратного уравнения (5.3) дает корни p₁ = - 3000 +j4000 c^-1;

p₂ = - 3000 - j4000 c^-1

Для определения оригинала используем следующий вид теоремы разложения:

_{, (5.4)}

_,

_,

_.

Подставив в полученные выражения p₁ = - 3000 +j4000 c^-1, получим:

.

Подставив рассчитанные значения в теорему разложения (5.4), получим:

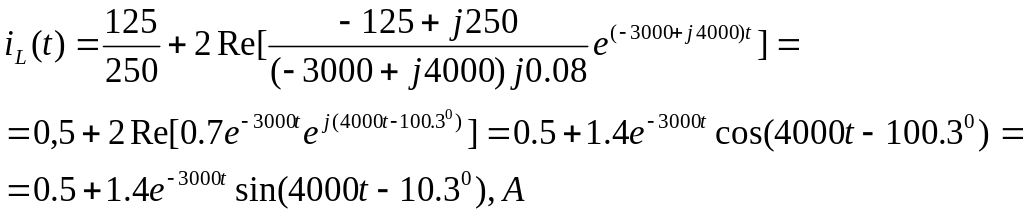_(5.5)

Определение корней характеристического уравнения (5.3) и функций входящих в теорему разложения (5.4), (5.5) можно произвести в среде MathСad изложенными выше способами.

При построении графика в среде MathCad рассчитаем время окончания переходного процесса t = 5τ = 5 = 5 =0,0017 c для определения наибольшего значения по оси х. Для определения порядка значений по оси у рассчитаем значения i_L(0) и i_Lсв(0) с помощью оператора «substitute» при t=0. Подробно методика построения графиков приведена в разделе 3 данного пособия.

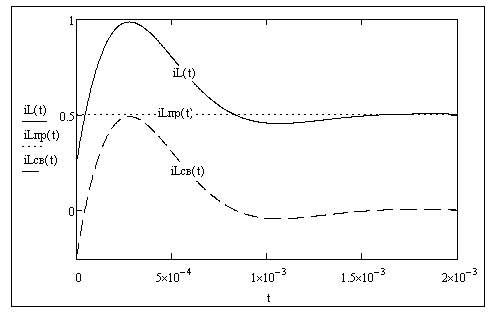
Рисунок 5.3

6 Расчет переходных процессов с помощью интеграла Дюамеля

На вход цепи (см. рисунок 6.1) с заданными параметрами R₁= R₃=40 Oм, R₂= 20 Oм, L = 10 мГн, U = 20 В, t_и = 4 мс подается импульс напряжения u(t) (см. рисунок 6.2). Определить ток i₂(t) в переходном режиме.

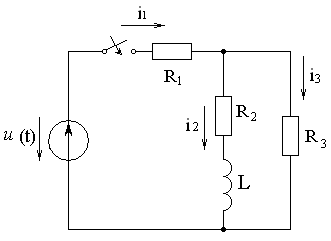
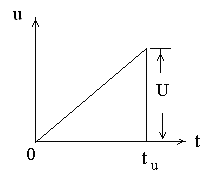
Рисунок 6.1 Рисунок 6.2

Этап1. Для определения переходной проводимости рассчитываем переходной процесс при подключении цепи при нулевых начальных условиях i₂(0)=0 к источнику единичного постоянного напряжения (см. рисунок 6.3) и определяем ток i₂(t).

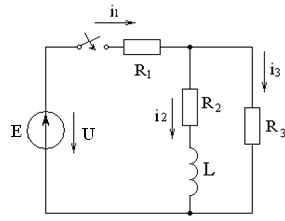
Рисунок 6.3

Ток i₂ в переходном режиме можно представить в виде i₂= i_2пр+ i_2св.

Определим принужденное значение тока i₂:

, А.

, А.

Для записи свободной составляющей найдем корни характеристического уравнения, составленного для послекоммутационной схемы относительно ветви с индуктивностью:

Таким образом,

При t=0: 0=0,0125Е+А, откуда, А=-0,0125Е, а значит

_.

Следовательно, переходная проводимость равна:

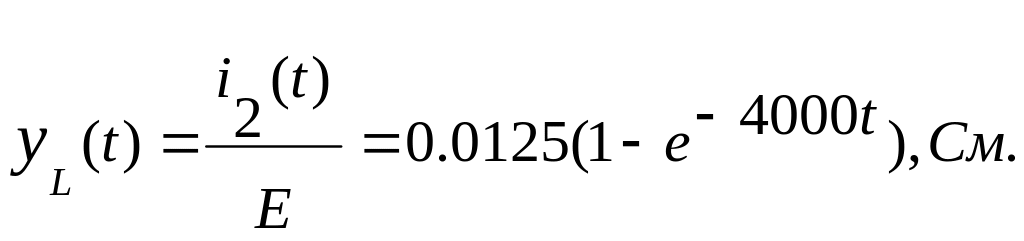
Этап 2. Определение тока i₂(t) в переходном режиме с помощью интеграла Дюамеля при подключении цепи на импульс напряжения u(t):

Рассчитаем i₂(t) в интервале времени , не включая скачка.

,

_,

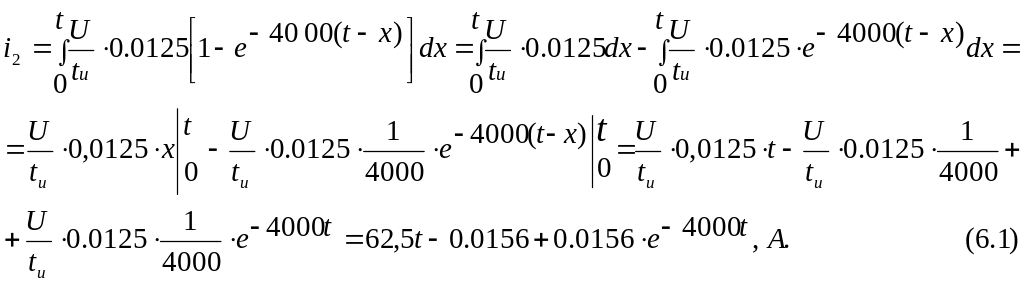
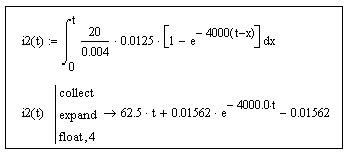
Проверить правильность расчета интеграла Дюамеля в среде MathCad в первом интервале можно с помощью операторов expand и collect.

Рассчитаем i₂(t) в интервале времени .

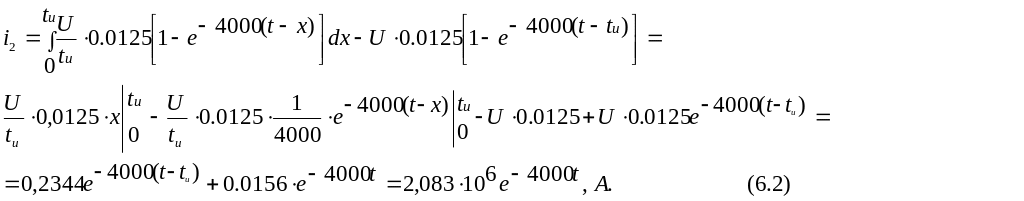
Проверить правильность расчета интеграла Дюамеля в среде MathСad во втором интервале можно с помощью операторов expand и collect.

График i₂(t) представляет собой кусочно-непрерывную функцию, заданную на первом интервале выражением (6.1) и на втором интервале выражением (6.2). График строится в интервале времени от 0 до 2t_u. Для определения порядка значений по оси Y рассчитаем значения i₂(t_u) для обоих интервалов с помощью оператора «substitute» при t= t_u= 0.004c, где i₂₁(t)- значение тока i₂(t) в первом интервале, i₂₂(t)- значение тока i₂(t) во втором интервале. Подробно методика построения графиков изложена в разделе 3 данного пособия.

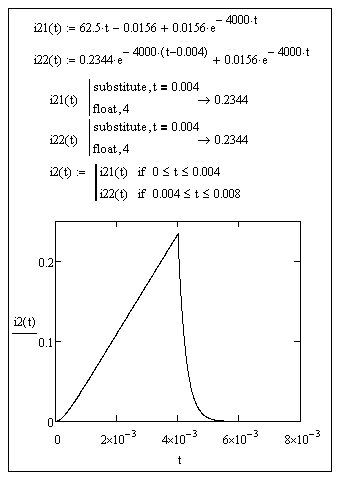
Рисунок 6.4

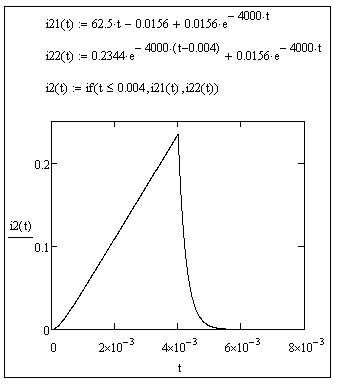
Рисунок 6.5