4 Расчет переходных процессов классическим методом

И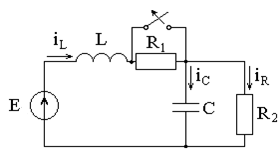 сходные данные:

Е=2000 В

С = 100 мкФ

R₁=R₂=100 Ом

L =1 Гн

Определить ток i_R в переходном

режиме.

Рисунок 4.1

При расчете переходных процессов классическим методом ток в переходном режиме в ветви с активным сопротивлением можно представить:

i_R = i_Rпр+ i_Rсв.

Принужденная составляющая тока i_Rпр = =10А.

Для определения корней характеристического уравнения воспользуемся методом входного сопротивления :

(4.1)

В среде MathСad присвоим параметрам цепи заданные в задаче числовые значения.

Выражение (4.1) приведем к виду рациональной дроби, числитель и знаменатель которой являются многочленами относительно p, с помощью оператора «collect», который находится на панели «Символика».

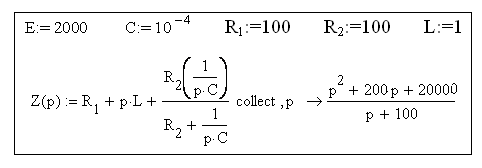
(4.2)

Для нахождения корней p₁ и p₂ характеристического уравнения приравняем выражения (4.2) к нулю и определим корни с помощью оператора «solve», который находится на панели «Символика» и применяется для решения уравнений в численном или символьном виде. Для ограничения количества значащих единиц следует ввести команду «float» и после запятой указать число значащих цифр, например 4. Чтобы появился результат необходимо щелкнуть левой кнопкой мыши по пустому месту.

Таким образом, корни характеристического уравнения комплексно-сопряженные: p₁= –100 + j100 с^-1, p₂ = –100 – j100 с^-1, где α=100 с^-1, ω_св=100рад/с.

Для комплексно- сопряженных корней свободная составляющая искомого тока имеет следующий вид:

i_Rсв= Ае^-αt sin(ω_свt + ψ) =Ае^-100t sin(100t + ψ). (4.3)

Запишем уравнения искомого тока и его производной:

i_R= 10 + Ае^-100t sin(100t + ψ) (4.4)

= Ае^-100t [-100sin(100t + ψ) +100cos(100t + ψ)].

Запишем систему (4.4) для момента времени t=0:

i_R(0) = 10 + Аsinψ (4.5)

(0) = –100 Аsinψ +100 Асos ψ.

Определим по законам коммутации независимые начальные условия i_L(0) и u_C(0):

i_L(0) = i_L(0_-) = = 20 А; u_C(0) = u_C(0-) = =2000 В.

Для определения постоянных интегрирования найдем зависимые начальные условия i_R(0) и (0) из законов Киргофа, записанных для момента времени t=0:

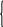i_R(0)R₂ – u_c(0) =0 (4.6)

i_L(0) – i_R(0) – i_c(0) = 0. (4.7)

Из уравнения (4.6) найдем i_R(0) = = 20 A.

Из уравнения (4.7) найдем i_c(0) = i_L(0) – i_R(0) = 0.

Перепишем уравнение (4.6) для произвольного момента времени:

i_RR₂ – =0.

Продифференцируем полученное выражение:

_.

Перепишем последнее выражение для момента времени t = 0 и выразим :

, откуда _.

Подставим в cистему (4.5) зависимые начальные условия:

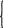20 = 10 + Аsinψ (4.8)

0 = –100 Аsinψ +100 Асosψ.

Из (4.8) определим Аsinψ = 10, Асosψ = 10, ψ = arctg = 45⁰, А = 14,1

Запишем выражение тока в переходном режиме:

i_R= 10 + 14,1е^-100t sin(100t + 45⁰), А (4.9)

Для построения графика переходного тока i_R в среде MathСad в интервале времени от 0 до t = 5τ рассчитаем время окончания переходного процесса при t = 5τ = 5 = 5 =0,01 c . Таким образом, максимальное значение по оси х равно 0,01с. Для определения наибольшего значения по оси у рассчитаем значение i_R(0) с помощью оператора «substitute» при t=0. Этот оператор находится на панели «Символика» и применяется для решения уравнений в численном или символьном виде при заданном значении переменной. Подробно методика построения графиков приведена в разделе 3 данного пособия.

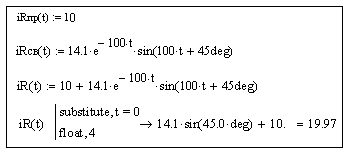
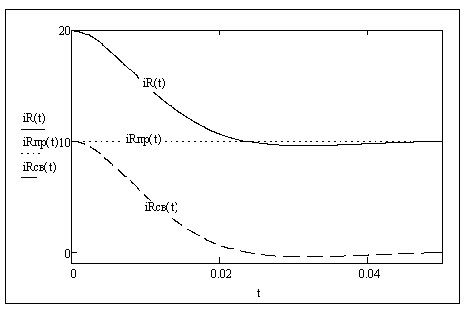
Рисунок 4.2