3.5 Построение двумерных графиков функций, заданных таблично

При дискретном изменении аргумента, связь между аргументом и функцией задается в виде таблицы. Табличные значения функции могут быть получены как расчетным путем, так и экспериментально. Например, функция дискретного аргумента задана в виде таблицы 3.5.1. Для построения графиков функций, заданных таблично, аргумент и функция записываются в виде матриц-столбцов с N строками, для приведенного примера N=5.

Таблица 3.5.1 - Функция у(х) задана таблично.

х	0	3	6	9	12
у	0	8	5	7	20

Если диапазон изменений аргумента (ось абсцисс) и функции (ось ординат) не указывать, то предельные значения аргумента и функции определяются их минимальными и максимальными значениями. На полученном графике (см. рисунок 3.18,а) точки соединяются по умолчанию, отрезками прямой. Для построения графика без линейной интерполяции значений во вкладке Traces (линии графика) в пункте Type (установка типа графика) выбирают тип stem (построение вертикальными черточками) и в пункте Symbol (символ) выбирают символ для отметки расчетных точек на графике, например, +'s − прямой крестик (см. рисунок 3.18,б и пример 3.6.2)

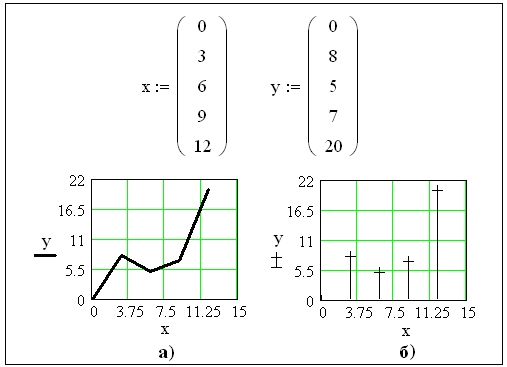
Рисунок 3.18 - Построение графика функции, заданной таблично

3.6 Примеры построения графиков

Пример 3.6.1. Построение графиков токов и напряжений в цепи синусоидального тока.

В линейной электрической цепи при гармонических воздействиях токи в ветвях и напряжения на любом участке цепи изменяются по синусоидальному закону. Построим, графики тока и напряжения , где ω=2πf, f=50Гц, начальные фазы тока и напряжения заданы в градусах. Для правильного построения графиков в MathСad после значений начальных фаз, заданных в градусах, нужно напечатать deg или перевести градусы в радианы. Выберем в качестве аргумента время t. Диапазон значений аргумента выберем от 0 до 2Т, где Т=1/f=0,02с – период. Предельные значения по оси ординат выберем немного больше амплитудных значений тока и напряжения (см. рисунок 3.19). Можно выбрать в качестве аргумента ωt, диапазон значений аргумента от 0 до 4π – что соответствует двум периодам (см. рисунок 3.20).

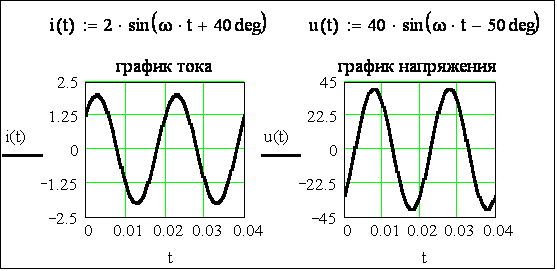
Рисунок 3.19 - Графики синусоидальных тока и напряжения

(аргумент – время t)

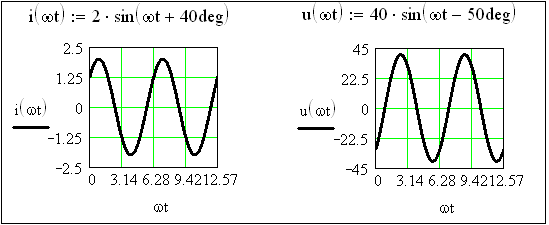
Рисунок 3.20 - Графики синусоидальных тока и напряжения

(аргумент – ωt)

Пример 3.6.2. Построение графиков токов и напряжений в электрической цепи несинусоидального периодического тока.

В линейной электрической цепи с несинусоидальными периодическими

источниками питания токи в ветвях и напряжения на любом участке цепи также будут несинусоидальными периодическими функциями времени. Несинусоидальные периодические токи и напряжения могут быть представлены тригонометрическим рядом Фурье:

.

Построим график мгновенного несинусоидального периодического тока:

, = 0,2026 А – постоянная составляющая тока;

А − первая гармоника тока;

А – вторая гармоника тока.

Обязательно должны быть построены графики отдельных гармоник и график несинусоидального периодического тока, который получается суммированием графиков отдельных гармоник (см. пункт 3.2 Построение в одном шаблоне графиков нескольких функций). При построении графиков выберем в качестве аргумента ωt, диапазон значений аргумента от 0 до 4π. Предельные значения тока по оси ординат выберем немного больше максимального значения тока i(t). График тока каждой гармоники и суммарный график несинусоидального периодического тока отформатируем, используя вкладку Traces (линии графика), пункт Line –установка типа линий графика (см. 3.4.3 Traces и см. рисунок 3.21,а).

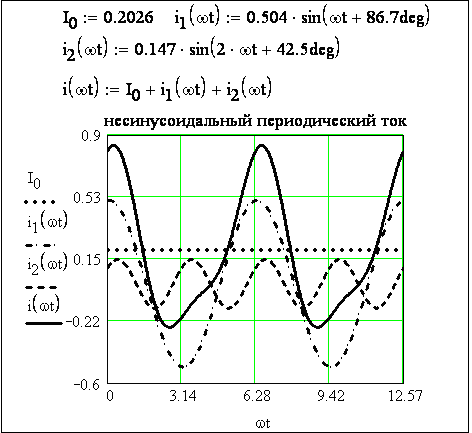
Рисунок 3.21,а - График несинусоидального периодического тока

Построим амплидутно-частотный и фазо-частотный спектры (см. пункт 3.5). Зависимость от частоты амплитудных значений гармонических составляющих несинусоидального периодического тока задана в виде таблицы 3.2, где основная частота принята равной 400 рад/с.

Таблица 3.2 - Амплидутно-частотный спектр несинусоидального тока.

ω рад/с	0	400	2·400
Imk, А	0,2026	0,504	0,147

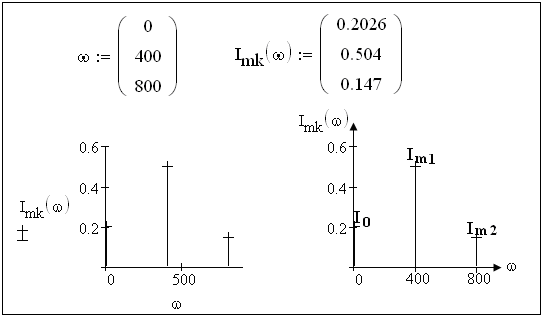
Рисунок 3.21,б - Амплидутно-частотный спектр

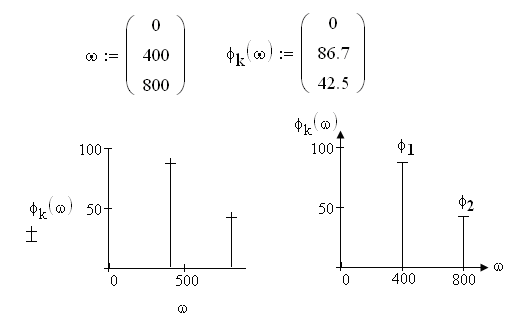
Рисунок 3.21, в - Фазо-частотный спектр

Зависимость от частоты начальных фаз гармонических составляющих задана в виде таблицы 3.3.

Таблица 3.3 - Фазо-частотный спектр несинусоидального тока

ω рад/с	0	400	2·400
φk, град.	0	86,7	42,5

Графики амплидутно-частотного спектра и фазо-частотного спектра несинусоидального тока, построены в MathСad и отредактированы в Paint (см. рисунки 3.21, б, в).

Пример 3.6.3. Построение графиков переходных токов и напряжений.

Построим графики токов и напряжений в переходном режиме в цепях второго порядка. Выражение свободной составляющей (тока или напряжения) зависит от вида корней характеристического уравнения:

для вещественных и различных корней < 0 и < 0

,

для вещественных и равных корней = =р < 0

,

для комплексно-сопряжённых корней (α – коэффициент затухания, ω_СВ – частота свободных колебаний)

.

а) Построение графиков переходных тока и напряжения в цепях второго порядка при постоянном источнике питания для случая, когда корни характеристического уравнения вещественные и различные:

− переходное напряжение на емкости, − принужденное напряжение на емкости; − свободное напряжение на емкости;

− переходный ток в емкости.

При построении графиков диапазон значений аргумента выбираем от 0 до 5τ_mах, где τ_mах=1/500 с=0,002 с –максимальное значение постоянной времени цепи. На рисунке 3.22 показан график переходного тока, предельные значения ординаты выбраны больше максимальных значений тока.

На рисунке 3.23 показано построение в одном шаблоне графиков принужденного, свободного и переходного напряжения на емкости (см. пункт 3.2 Построение в одном шаблоне графиков нескольких функций), предельные значения ординаты выбраны больше максимальных значений напряжений. Графики напряжений и тока отформатированы с использованием вкладки Traces, .

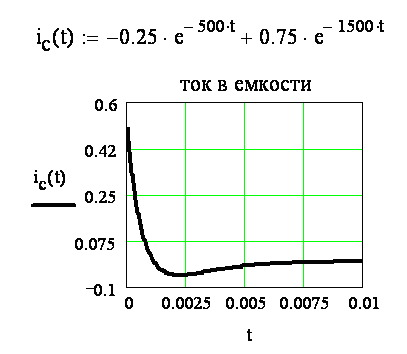
Рисунок 3.22 - Переходный ток в емкости

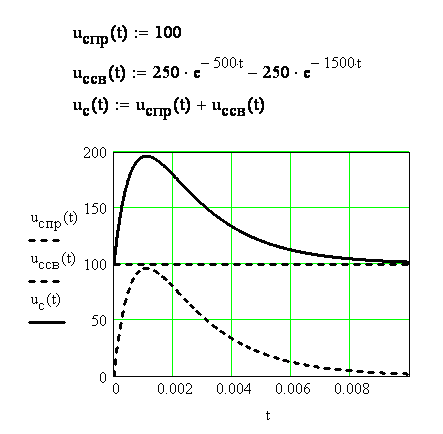
Рисунок 3.23 - Переходное напряжение на емкости

б) Построение графиков переходных тока и напряжения в цепях второго порядка при постоянном источнике питания для случая, когда корни характеристического уравнения комплексно-сопряженные.

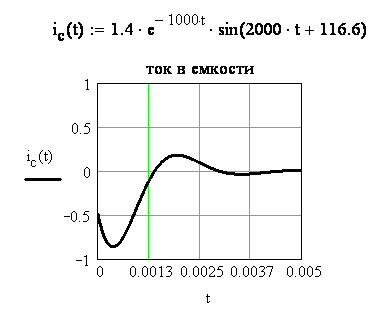
Рисунок 3.24 - Переходный ток в емкости

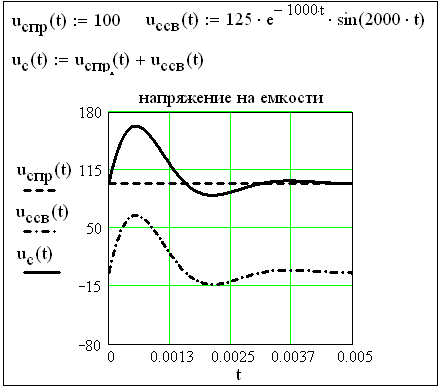
Рисунок 3.25 - Переходное напряжение на емкости

Ток и сводное напряжение на емкости изменяются по гармоническому закону:

− переходный ток в емкости;

− переходное напряжение на емкости;

− принужденное напряжение на емкости;

− свободное напряжение на емкости.

При построении графиков диапазон значений аргумента выбираем от 0 до 5/α, где α=1000 – коэффициент затухания. На рисунке 3.24 показан график переходного тока на емкости, на рисунке 3.25 показано построение графиков принужденного, свободного и переходного напряжения на емкости.

Пример 3.6.4. Интеграл Дюамеля. Построение графиков переходного тока и переходного напряжения.

Пусть электрическая цепь (см. рисунок 3.26), параметры которой равны: подключается к источнику напряжения с максимальным значениями U_M=20 В длительностью t_u=4мс (см.рисунок 3.27).

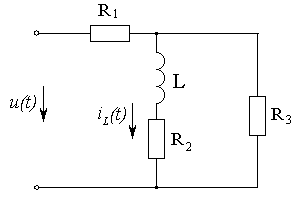
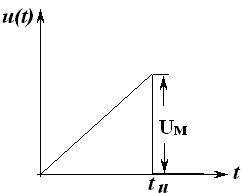
Рисунок 3.26 - Электрическая схема Рисунок 3.27 - Напряжение источника

Ток и напряжение на индуктивности были определены с помощью интеграла Дюамеля, и представляют собой кусочно-непрерывные функции времени:

в интервале ;

=

в интервале .

в интервале ;

=

в интервале .

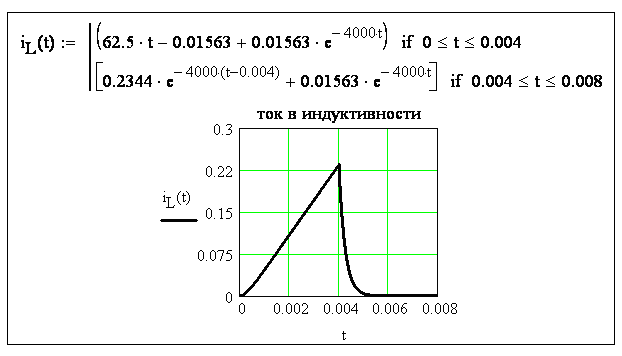
Рисунок 3.28 - График тока в индуктивности

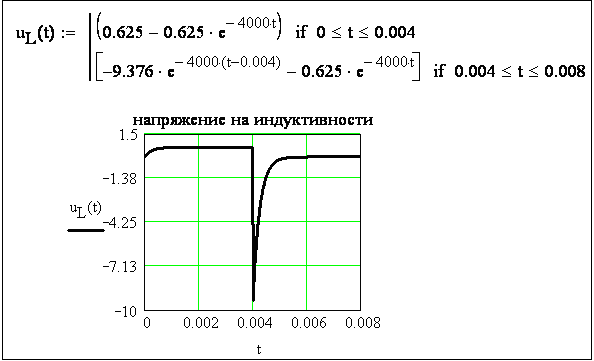
Рисунок 3.29 - График напряжения на индуктивности

Построение в MathСad графиков тока и напряжения показано на рисунках 3.28 и 3.29. (см. пункт 3.3 Построение графиков кусочно-непрерывных функций).

Как видно из графика (см. рисунок 3.28), ток в момент времени t=t_u скачком не изменяется (согласно закону коммутации), в то время как напряжение источника в этот момент времени уменьшается скачком от до 0. Как видно из графика (см. рисунок 3.29), напряжение в момент времени t=t_u изменяется скачком. Диапазон значений аргумента выбираем от 0 до 2∙t_u.(здесь t_u=0,004с). Предельные значения ординат принимаем немногим больше максимальных (по абсолютной величине) значений, соответственно, тока и напряжения _.

Пример 3.6.5. Построение графиков амплитудно-частотных характеристик (АЧХ) и фазо-частотных характеристик (ФЧХ) передаточных функций электрической цепи.

Для электрической цепи (см. рисунок 3.30) с параметрами комплексная передаточная функция цепи по напряжению , АЧХ и ФЧХ имеют вид:

АЧХ:

ФЧХ:

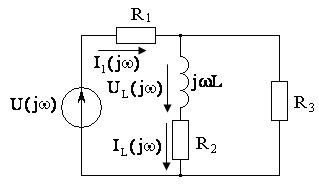
Рисунок 3.30 - Электрическая схема

На рисунках 3.31, 3.32 показаны графики АЧХ и ФЧХ, построенные в MathCad. Диапазон значений аргумента ω выбран от 0 до 4 ω_ГР (где ω_ГР определено из условия (ω/10000)=1). Диапазон значений ординаты для АЧХ выбран от 0 до 0.4, для ФЧХ – от 2 радиан (максимальное значение ФЧХ = π/2 для частоты ω = 0) до 0. Для выбора предельных значений ординаты при построении графика АЧХ определим значения для частот ω = 0 и ω = ∞: , .Для выбора предельных значений ординаты при построении графика ФЧХ определим значения для частоты ω = 0 и ω = ∞: , .

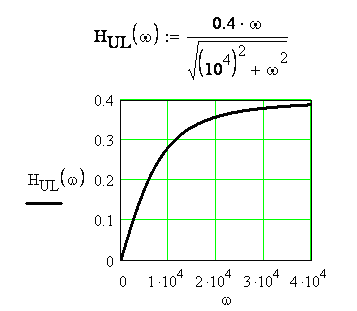
Рисунок 3.31 - График АЧХ

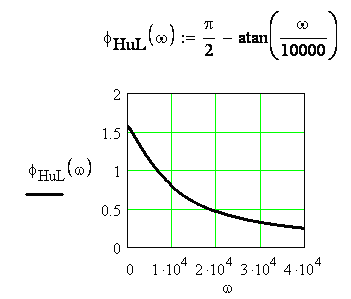
Рисунок 3.32 - График ФЧХ

Пример 3.6.6 Спектральный метод. Построение графиков АЧХ и ФЧХ спектров непериодических входных воздействий

Построим графики АЧХ, ФЧХ спектров непериодических входных воздействий в виде прямоугольного видеоимпульса с амплитудой и длительностью , t₀=0.4мс (см. рисунки 3.33, 3.34, 3.35).

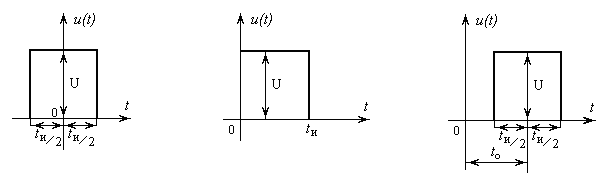
Рисунок 3.33 Рисунок 3.34 Рисунок 3.35

а) Спектр , АЧХ и ФЧХ для видеоимпульса (см. рисунок 3.33) имеют вид:

, АЧХ: ,

0 , если ,

ФЧХ:

π , если .

Построение графика АЧХ показано на рисунке 3.36. Диапазон значений аргумента выбран от ω = 0 до ω = 10π/t_u (значение частоты ω = 10π/t_u соответствует значению аргумента синуса ). Диапазон значений ординаты выбран от =0 до > t_uU.

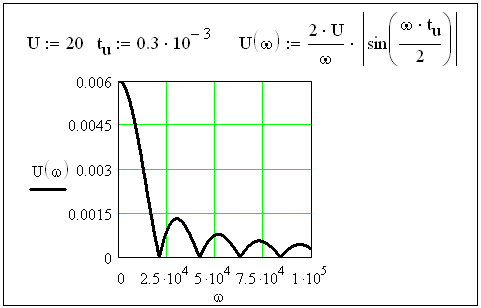
Рисунок 3.36 - График АЧХ входного воздействия

Построение графика ФЧХ φ(ω) для входного воздействия показано на рисунке 3.37. Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ. Диапазон значений ординаты φ(ω) выбран от φ(ω)=0 до φ(ω)=4рад. Алгоритм построения графика ФЧХ φ(ω) такой же, как построение графика кусочно-непрерывной функции (пункт 3.3).

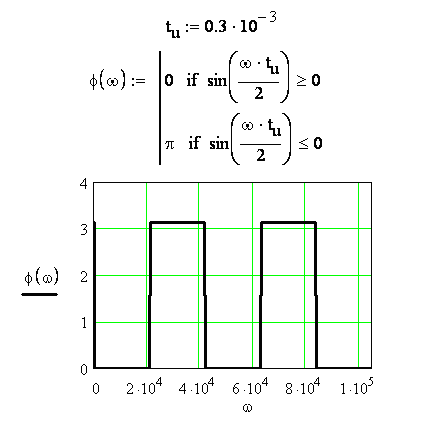
Рисунок 3.37- График ФЧХ входного воздействия φ(ω)

б) Спектр , АЧХ и ФЧХ для видеоимпульса (см. рисунок 3.34) имеют вид:

,

АЧХ ,

, если ,

ФЧХ

+ π , если .

График АЧХ показан на рисунке 3.36, т.е. имеет такой же вид, как для входного воздействия (см. рисунок 3.33).Построение графика ФЧХ φ(ω) входного воздействия показано на рисунке 3.38.

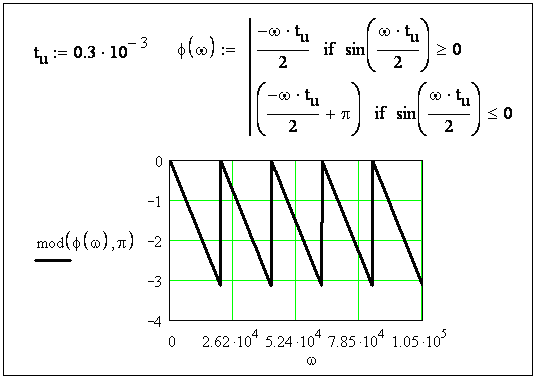
Рисунок 3.38 - График ФЧХ входного воздействия φ(ω)

Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ, от ω = 0 до ω = 10π/t_u.

При построении графика ФЧХ желательно, чтобы угол φ(ω) не превышал π. В связи с этим рекомендуется применить функцию mod(x, y) − остаток от деления х на у, результат имеет тот же знак, что и х. Для случая построения графика ФЧХ: mod(φ(ω), π). Диапазон значений ординаты φ(ω) выбран от φ(ω)=0 до φ(ω)=− 4рад.

в) Спектр , АЧХ и ФЧХ для видеоимпульса (см. рисунок 3.35) имеют вид:

,

АЧХ ,

, если ,

ФЧХ

+ π , если .

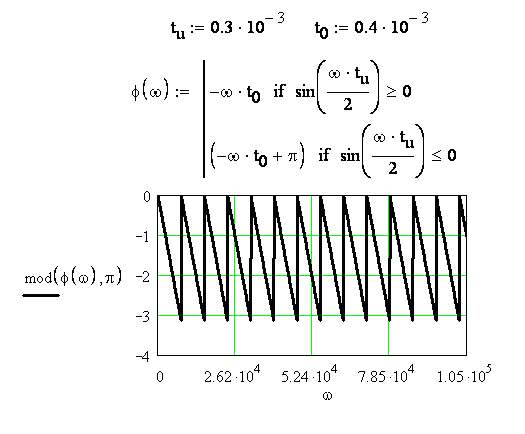
Рисунок 3.39 - График ФЧХ входного воздействия φ(ω)

График АЧХ показан на рисунке 3.36, т.е. имеет такой же вид, как для входного воздействия (см. рисунок 3.33). Построение графика ФЧХ φ(ω)

входного воздействия показано на рисунке 3.39.

Пример 3.6.7 Спектральный метод. Построение графиков АЧХ и ФЧХ спектров реакции цепи.

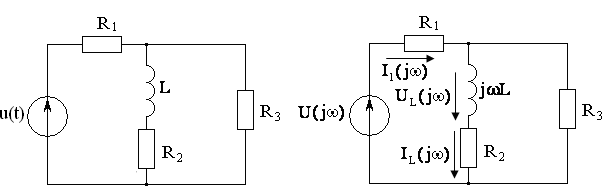
а) б)

Рисунок 3.40 - Схемы электрической цепи

Построим графики АЧХ и ФЧХ для спектральной плотности напряжения на индуктивности , если электрическая цепь (см. рисунок 3.40), параметры которой подключена к источнику непериодического напряжения u(t) в виде прямоугольного видеоимпульса с амплитудой и длительностью (см. рисунок 3.34).

Спектральная плотность напряжения на индуктивности определяется по формуле: , где − комплексная передаточная функция цепи по напряжению (см. пример 3.6.5), АЧХ и ФЧХ которой равны: ,

− спектр входного напряжения (см. пример 3.6.6), АЧХ и ФЧХ которого равны: ,

, если

+ π , если .

АЧХ напряжения на индуктивности определим как произведение АЧХ комплексной передаточной функции на АЧХ входного напряжения :

ФЧХ напряжения на индуктивности определим как сумму ФЧХ комплексной передаточной функции и ФЧХ входного напряжения :

, если ,

+ π , если .

Построение графика АЧХ показано на рисунке 3.41. Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ входного напряжения: от ω = 0 до ω = 10π/t_u. Диапазон значений ординаты выбран от 0 до 0,0015 (максимальное значение примерно равно 0,00117 В).

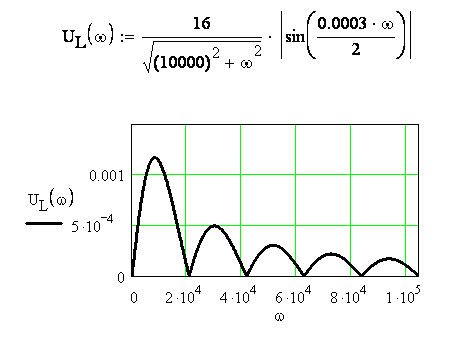
Рисунок 3.41- График АЧХ реакции цепи

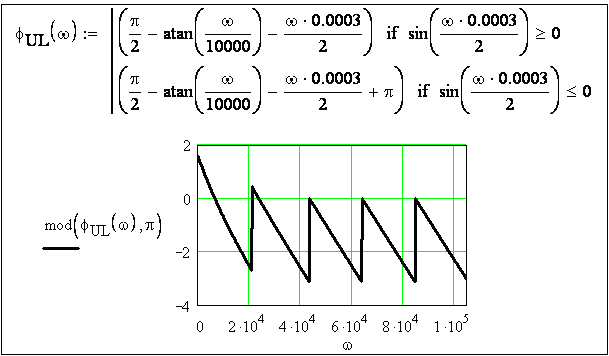
Рисунок 3.42 - График ФЧХ реакции цепи

Построение графика ФЧХ показано на рисунке 3.42. Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ входного напряжения: от ω = 0 до ω = 10π/t_u. Диапазон значений ординаты φ_UL(ω) выбран от 2 рад до − 4рад.