3 Построение графиков функций в Mathcad

При анализе установившихся и переходных режимов в электрических цепях большое значение имеет графическое представление результатов расчетов. Наглядность графиков токов и напряжений в электрических цепях позволяет всесторонне исследовать и интерпретировать полученные результаты.

Для построения графиков в MathCad используются соответствующие шаблоны, перечень которых содержит подменю График (Graph) в пункте главного меню Вставка (Insert) или панель Графики (Graph) — вставка шаблонов графиков (см. рисунок 3.1).

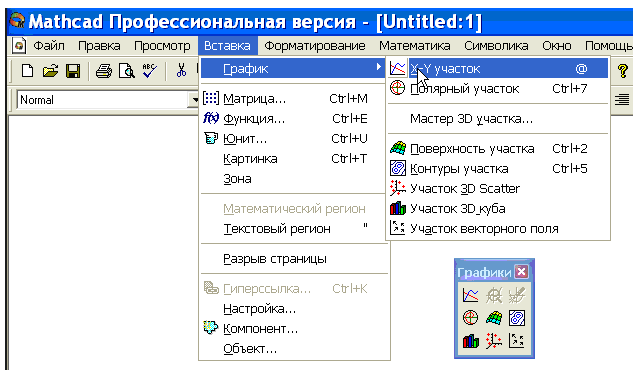
Рисунок 3.1 - Шаблоны для построения графиков и панель «Графики (Graph)»

3.1 Построение двумерных графиков функций, заданных аналитическими выражениями

3.1.1 Ввести аналитическое выражение функции, например:

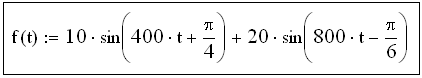
3.1.2 Задать диапазон значений аргумента, например:

.

Диапазон изменения аргумента состоит из 3-х значений: начальное, второе и конечное. В приведенном примере 0 − начальное значение диапазона аргумента, 0,0001− второе значение диапазона аргумента (0+0.0001 – начальное значение диапазона плюс шаг), 0.02 – конечное значение диапазона аргумента. Многоточие вводится с клавиатуры нажатием кнопки: точка с запятой (язык английский).

3.1.3 Установить курсор (крестик) в то место, где надо построить график.

3.1.4 В подменю График (Graph) или на математической панели щелкнуть по кнопке (см. рисунок 3.1).

3.1.5 На месте курсора появляется шаблон графика (см рисунок 3.2, а)

3.1.6 В шаблоне графика ввести на оси абсцисс имя аргумента, на оси ординат имя функции (см. рисунок 3.2, б).

а б

Рисунок 3.2 - Шаблон графика

3.1.7 Щелкнуть мышью вне шаблона графика. Появится график, построенный в заданном диапазоне изменения аргумента (см. рисунок 3.3).

Рисунок 3.3 - График функции f(t) в заданном диапазоне значений аргумента

Если график не принимает требуемый вид, нужно изменить шаг, диапазон значений аргумента и функции.

3.1.8 Если диапазон значений аргумента предварительно не задан, то предельные значения аргумента (на оси абсцисс) и предельные значения функции (на оси ординат) можно задать путем заполнения крайних меток на шаблоне графика, которые задают масштаб графика (см. рисунок 3.2, б). После заполнения предельных значений аргумента и функции (см. рисунок 3.4, а), щелкнуть мышью вне шаблона графика. Появится график, построенный для заданных предельных значений аргумента и функции (см. рисунок 3.4, б).

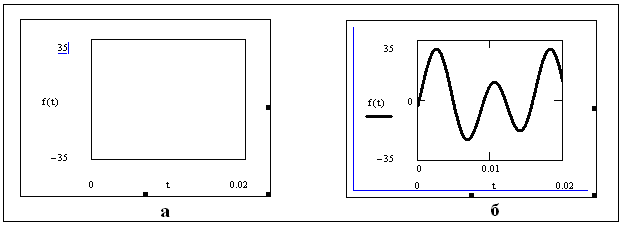
Рисунок 3.4 - График функции f(t) для заданных предельных значений аргумента и функции

3.1.9 Если диапазон значений аргумента предварительно не задан или не заполнены крайние метки на шаблоне графика, то график будет построен по умолчанию в диапазоне значений аргумента от −10 до 10, а предельные значения на оси ординат будут установлены больше максимальных расчетных значений функции (см. рисунок 3.5, а).

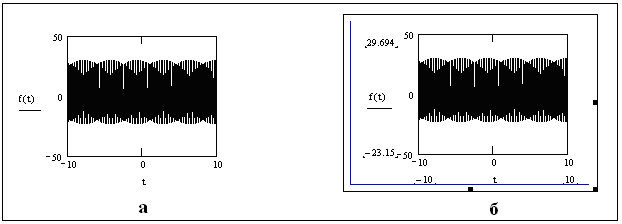
Рисунок 3.5- График функции f(t), построенный по умолчанию в диапазоне значений от −10 до 10

3.1.10 Диапазон значений аргумента, установленный по умолчанию от −10 до 10 в большинстве случаев не отражает график в требуемом виде, поэтому предельные значения аргумента по оси абсцисс и предельные значения функции по оси ординат изменяются вручную. Для этого график выделяют, щелкнув по графику мышью (см. рисунок 3.5, б).

3.1.11 На выделенном графике заменяют числа −10, например, на 0, а 10 на 0,02. Предельные значения на оси ординат устанавливают, например, − 35, 35 (см. рисунок 3.6, а). После установки нужных интервалов изменения аргумента и функции, щелкают мышью вне шалона графика. Появится график функции f(t), построенный в требуемом диапазоне значений аргумента (см. рисунок 3.6, б).

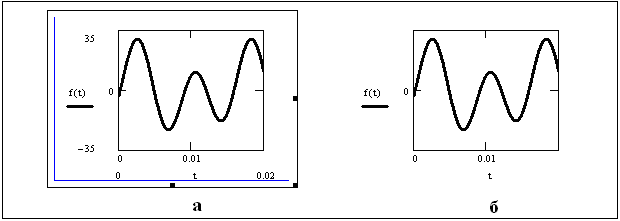
Рисунок 3.6 - График функции f(t)