МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РЕСПУБЛИКИ КАЗАХСТАН

Некоммерческое акционерное общество

“Алматинский университет энергетики и связи ”

З.И. Жолдыбаева

Е.Х. Зуслина

Применение mathcad в теории электрических цепей

Учебное пособие

Алматы 2012

УДК 621.3.71:519.6(275.8)

ББК 31.211 Я73

Ж 79. Учебное пособие. З.И. Жолдыбаева, Е.Х. Зуслина.

Применение MathCad в теории электрических цепей.

АУЭС. Алматы, 2012. - 83 с.

I SBN 978-601-7327-18-7

В пособии рассмотрены расчеты сложных разветвленных электрических цепей постоянного и синусоидального токов, расчет переходных процессов классическим, операторным, спектральным методами, с помощью интеграла Дюамеля и построение графиков функций в среде MathCad.

Пособие предназначено для студентов специальностей бакалавриата 5В071900, 5В070400, 5В070300, 5В074600, 5В060200, 5В071600, 5В100200.

Табл.4, ил.74, библиогр. - 16 назв.

ББК 31.211 Я73

РЕЦЕНЗЕНТЫ: КазНТУ канд. техн. наук. доц. Иманбекова Т.Д.

Печатается по плану издания Министерства образования и науки Республики Казахстан на 2012 г.

I SBN 978-601-7327-18-7

©НАО «Алматинский университет энергетики и связи», 2012г.

Введение

Теория электрических цепей является базовым курсом, на который опираются профилирующие дисциплины радиотехнических специальностей, специальностей по вычислительной технике и информационным системам. В соответствии с новыми учебными планами курс ТЭЦ изучается в течение двух семестров. При этом существенно увеличен объем самостоятельной работы студентов (до 60% от общего числа часов). Цель настоящего учебного пособия состоит в оказании помощи студентам в их самостоятельной работе.

В пособии рассмотрены расчеты сложных разветвленных электрических цепей постоянного и синусоидального токов, расчет переходных процессов классическим, операторным, спектральным методами, с помощью интеграла Дюамеля и построение графиков функций в среде MathCad. Расчеты и графики, выполненные в среде MathCad, в тексте выделены прямоугольными рамками.

Данное пособие рассчитано на студентов специальностей бакалавриата 5В071900, 5В070400, 5В070300, 5В074600, 5В060200, 5В071600, 5В100200. Оно ставит задачу помочь студентам в успешном изучении курса «Теория электрических цепей » и выполнении расчетно-графических и курсовых работ.

1 Расчёт сложных разветвленных электрических цепей

постоянного тока

Расчет сложных разветвленных цепей постоянного тока основан на решении системы линейных алгебраических уравнений (СЛАУ), составляемых по законам Кирхгофа, методу контурных токов, методу узловых потенциалов.

В общем случае система линейных алгебраических уравнений имеет вид:

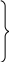
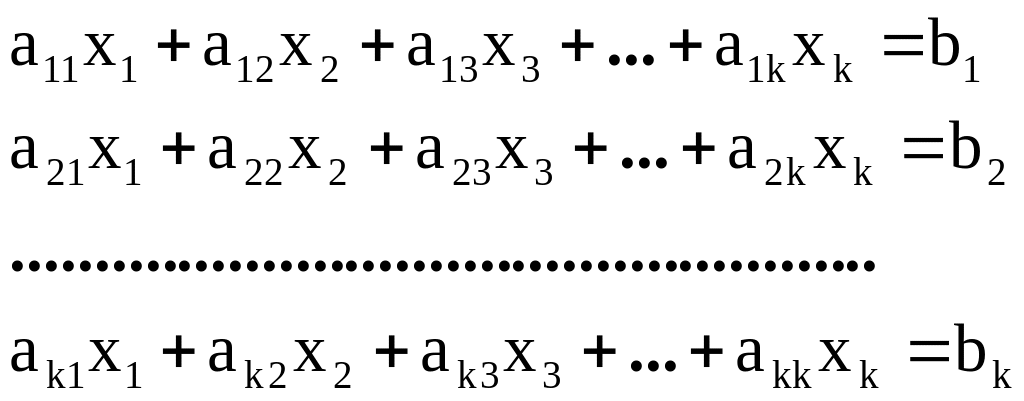, (1.1)

где коэффициенты при неизвестных переменных , свободные члены − постоянные действительные числа.

В MathCad СЛАУ можно решить различными способами.

Способ 1.1. Решение СЛАУ с помощью вычислительного блока given–find (см. пример 1.1):

− напечатать ключевое слово given (дано);

− ввести уравнения, входящие в систему, ниже ключевого слова given, между левой и правой частями уравнения поставить жирный знак логического равенства, для его ввода используют сочетание клавиш Ctrl = или выбирают его в панели Boolean (Булевый, Логический (см. рисунок 1.1));

− напечатать функцию find(x₁, x₂, x₃ …), где x₁, x₂, x₃ — неизвестные переменные;

− после find(x₁, x₂, x₃ …) поставить команду float (численное вычисление) и после запятой ввести число значащих цифр, затем щелкнуть левой кнопкой мыши по пустому месту и нажать знак равенства. Команду float можно напечатать или выбрать на панели Symbolic (Символика) (см. рисунок 1.1 и пример 1.1).

Пример 1.1

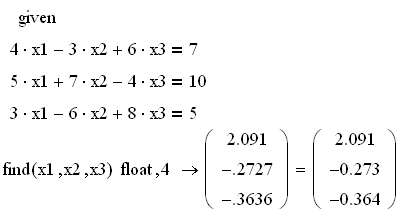
Способ 1.2. Решение СЛАУ с помощью оператора solve:

− в математическом меню выбрать кнопку с изображением матрицы. Откроется панель Matrix (Матрица) (см. рисунок 1.1), на которой щелкнуть по кнопке с изображением матрицы;

− откроется окно Insert Matrix (диалоговое окно), открыть диалоговое окно можно также нажатием сочетания клавиш Ctrl+m. В диалоговом окне надо ввести число строк матрицы, равное числу уравнений системы и число столбцов матрицы равное 1 и щелкнуть левой кнопкой мыши по кнопке ОK. На экране появится шаблон матрицы;

− в каждой строке полученной матрицы записать одно уравнение из системы, между левой и правой частями уравнения поставить жирный знак равенства, используя сочетание клавиш Ctrl = или выбрав его в панели Boolean (Булевый, Логический);

− применить к системе уравнений, записанных в виде матрицы оператор solve.

Оператор solve находится на панели Symbolic (Символика) (см. рисунок 1.1) и применяется для решения уравнений или систем уравнений в численном и символьном виде. После solve,x1,x2,x3 можно вставить команду float, записать число значащих цифр, щелкнуть левой кнопкой мыши по пустому месту и нажать знак равенства (см. пример 1.2).

Пример 1.2

Рисунок 1.1 - Панели Символика, Булевый, Математика, Матрица

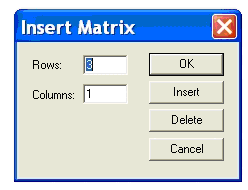
Рисунок 1.2 - Диалоговое окно Insert Matrix

Способ 1.3. Решение СЛАУ с помощью оператора lsolve (lsolve(А,В) – решение системы линейных уравнений):

− запишем СЛАУ в матричной форме , где А – матрица составленная из коэффициентов (i - номер строки матрицы, а j- номер столбца) при неизвестных переменных х₁,х₂,х₃…; В – матрица-столбец (вектор), составленная из свободных членов ; Х – матрица-столбец (вектор), составленная из неизвестных переменных х_i;

− чтобы присвоить значение переменной А, обозначающей матрицу коэффициентов, запишем сначала «А:=», а затем вставим матрицу коэффициентов уравнений ;

− чтобы присвоить значение переменной В, обозначающей матрицу свободных членов, запишем сначала «В:=», а затем вставим матрицу-столбец (вектор) свободных членов;

− запишем «Х:=lsolve(А,В)», где X – переменная, обозначающая матрицу-столбец неизвестных переменных х_i;

− для получения результата нужно напечатать Х и нажать знак = (см. пример 1.3).

Примечание. Оператор lsolve можно напечатать или щелкнуть левой кнопкой мыши по кнопке f(x) – список встроенных функций (см. рисунок 1.3), или используя сочетание клавиш Ctrl+E. Откроется диалоговое окно, в котором надо выделить оператор (функцию) lsolve и щелкнуть левой кнопкой мыши по кнопке ОK (см. рисунок 1.4);

Рисунок 1.3 - Панель инструментов (Standard)

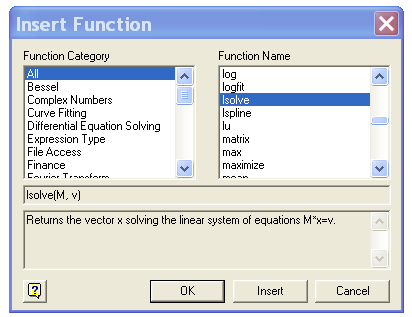
Рисунок 1.4 - Диалоговое окно Insert Function

Пример 1.3

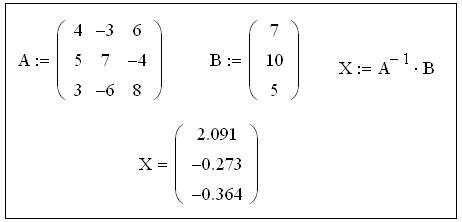
Способ 1.4. Решение СЛАУ путем обращения матрицы коэффициентов:

− запишем СЛАУ в матричной форме , где А – матрица составленная из коэффициентов (i – номер строки матрицы, а j – номер столбца) при неизвестных переменных х₁,х₂,х₃…; В – матрица-столбец, составленная из свободных членов ; Х – матрица-столбец, составленная из неизвестных переменных х_i;

− решим СЛАУ в матричной форме путем обращения матрицы коэффициентов X = A^-1 ·B (см. пример 1.4).

Пример 1.4

Примеры решения СЛАУ, составленные по МКТ и МУП приведены в задаче 1.1.

Примечание: для решения СЛАУ в MathCad выбирается произвольно один из рассмотренных выше способов.

Задача 1.1. Для электрической цепи (см. рисунок 1.5), содержащей независимые источники ЭДС , , , , независимый источник тока А, резистивные сопротивления Ом, Ом, Ом, Ом, Ом, выполнить следующее:

− рассчитать токи во всех ветвях методом контурных токов (МКТ);

− рассчитать токи во всех ветвях методом узловых потенциалов (МУП).

Рисунок 1.5 - Схема цепи постоянного тока

Расчет токов методом контурных токов.

Один контурный ток выберем так, чтобы он проходил через источник тока, тогда этот контурный ток совпадёт с током источника тока . В двух других независимых контурах цепи (не содержащих источник тока!) введем контурные токи (cм. рисунок 1.5).

Для двух неизвестных контурных токов составим уравнения по методу контурных токов:

. (1.2)

Перенесём в правую часть уравнения, получим:

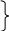
. (1.3)

Обозначим:

Запишем систему уравнений (1.3) в виде:

, (1.4)

Уравнение контурных токов в матричной форме имеет вид:

R _k I_k= E_k , (1.5)

где R_k– квадратная матрица контурных сопротивлений R_k= ; E_k– матрица-столбец контурных ЭДС: E_k= ;

I_k – матрица-столбец контурных токов: I_k= .

Решая систему уравнений (1.4), или уравнение контурных токов в матричной форме (1.5) в MathСad одним из приведенных способов, определим контурные токи: , . Токи в ветвях представим в виде алгебраической суммы контурных токов протекающим по этим же ветвям:

Ниже приведено решение системы контурных уравнений (1.4), (1.5) в MathCad различными способами.

Расчет токов методом узловых потенциалов. Примем и запишем уравнения для определения потенциалов :

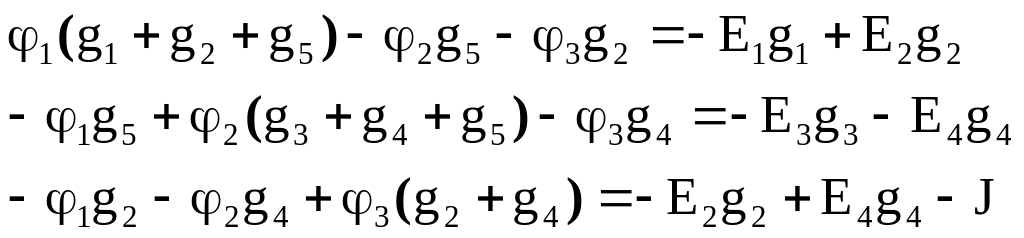
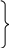, (1.6)

где

Обозначим:

Запишем систему уравнений (1.6) в виде:

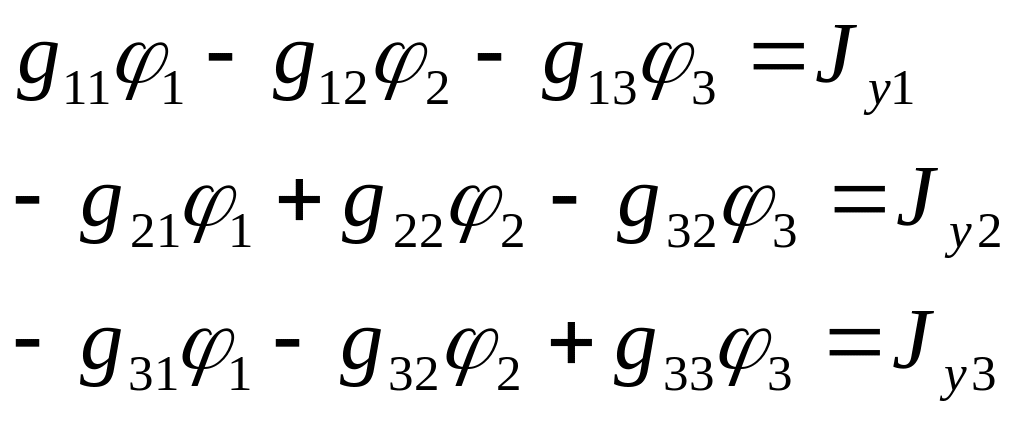
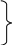_(1.7)

Уравнения узловых потенциалов в матричной форме: G_у φ_у = J_y (1.8)

где G_{y –} квадратная матрица узловых проводимостей:

G_{y = ;}

J_y – матрица-столбец узловых токов: J_{y= ;}

φ_у – матрица-столбец узловых потенциалов: φ_у= .

Решая уравнения узловых потенциалов в MathCad одним из приведенных способов, найдём потенциалы узлов электрической цепи:

Токи определим по закону Ома:

Ниже приведено решение системы уравнений по методу узловых потенциалов (1.7), (1.8) в MathCad различными способами.

Решение системы уравнений по методу контурных токов и узловых потенциалов в MathCad различными способами.

Присвоим параметрам цепи и источникам ЭДС и тока, заданные в задаче числовые значения:

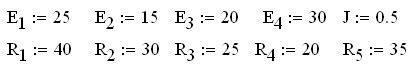
Присвоим:

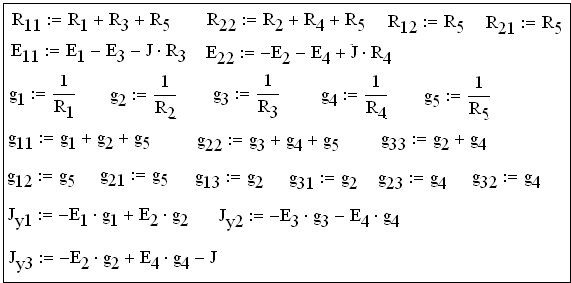
Способ 1.1. Решение СЛАУ с помощью вычислительного блока given–find.

Решение системы уравнений по методу контурных токов (1.4):

, .

Решение системы уравнений по методу узловых потенциалов (1.7):

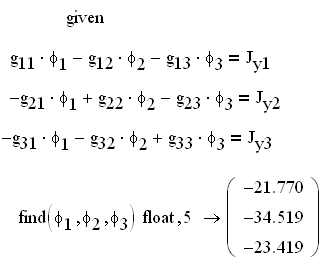
Способ 1.2. Решение СЛАУ с помощью оператора solve.

Решение системы уравнений по методу контурных токов (1.4):

, _.

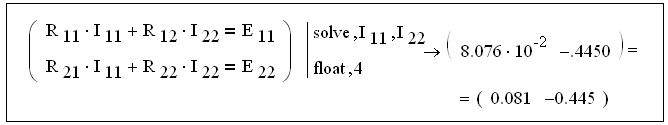
Решение системы уравнений по методу узловых потенциалов (1.7):

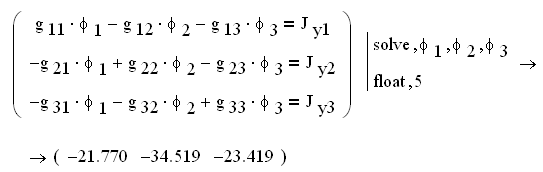
Способ 1.3. Решение с помощью оператора lsolve.

Решение системы уравнений по методу контурных токов в матричной форме R_k I_k= E_k с помощью оператора lsolve:

,

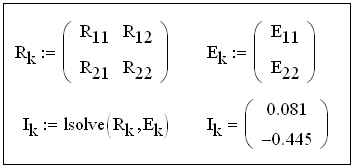
Решение системы уравнений по методу узловых потенциалов в матричной форме G_y φ_у = J_y с помощью оператора lsolve:

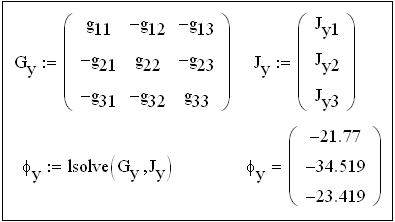
Способ 1.4. Решение путем обращения матрицы коэффициентов.

Решение системы уравнений по методу контурных токов в матричной форме R_k I_k= E_k

.

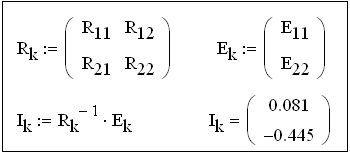
Решение системы уравнений по методу узловых потенциалов в матричной форме G_y φ_y = J_y

Примечание: 1. Нижний индекс переменной можно задать путем нажатия точки на клавиатуре (язык английский);

2. Простой способ ввода греческих букв: надо с клавиатуры набрать латинский аналог греческой буквы, как правило, первую букву в латинском названии греческой буквы, введя аналог греческой буквы, следует нажать сочетание клавиш Ctrl+G, на экране появится греческое написание буквы, заглавной или строчной в зависимости от того, в верхнем или в нижнем регистре был набран ее латинский аналог.

Греческие буквы и их аналоги (в скобках): α(a), β(b), χ(c), δ(d), ε(e), η(h), γ(g), λ(l), μ(m), ν(n), ω(w), ϕ(f), π(p), ψ(y), ρ(r), σ(s), τ(t), θ(q), ξ(x), ς(z).