Задание
Для статически неопределимой рамы (рис. 31) с заданными размерами и нагрузкой требуется построить эпюры изгибающих моментов, поперечных и продольных сил.
Обозначим
.
Тогда
Рис. 31
Примечание. На ригеле осевой момент инерции I1, на стойке I2.
Решение
Находим степень кинематической неопределимости рамы:
Здесь ny=2 (рамные узлы D и E).
Число независимых линейных смещений узлов nл находим как степень свободы шарнирно-стержневой системы, полученной введением шарниров во все узлы рамы.
Рис. 32
Для геометрической неизменяемости системы необходима дополнительная опорная связь в узле Е (или в узле D).
Отметим, что узлы D и E могут смещаться только по вертикали.
Таким образом,
Образуем основную систему (рис.33), введя связи, препятствующие возможным перемещениям узлов. Выбираем направления неизвестных перемещений и записываем систему канонических уравнений:
Рис. 33
Вычислим
погонные жёсткости
на каждом участке рамы:
;
;
Примем
за
, тогда
;
;
.
Найденные значения покажем на участках рамы.
Построим эпюры моментов от единичных перемещений введённых связей и от нагрузки, используя таблицы реакций из учебника (рис.34)
Рис.34
Реактивные моменты в первой и второй связях определяются вырезанием узлов D и E с введёнными связями, а реакцивное усилие в третьей связи способом разреза элементов рамы и рассмотрения уравнений равновесия отсечённой части.
Неизвестную реакцию (момент или силу) будем считать положительной, если её направление совпадает с принятым направлением поворота или линейного смещения узла.
Вырезаем
узлы D
и
E
на эпюрах
,
,
,
и из уравнений равновесия узла вида
находим коэффициенты и свободные члены
первых двух канонических уравнений.
Покажем,
например, определение
и
.
Узел
D
( эпюра
)
о
тсюда
Узел
Е
(эпюра
)
следовательно,
Рис.35
Аналогично определяются и другие реактивные моменты в связях 1 и 2. Выпишем результаты вычислений:
кН·м
кН·м
По теореме о взаимности реакций имеем:
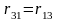и
.
Усилия
и
в 3-й связи находим с помощью сечения I
- I,
которое при разрезании участков рамы
выявляет поперечные силы, лежащие на
одной оси с определяемой реакцией.
Эпюра , сечение I – I.
Уравнение равновесия отсечённой части рамы:
следовательно,
Рис.36
Эпюра
откуда
кН
Рис.37
Система уравнений примет вид:
Решение этой системы даёт:
Для получения окончательной эпюры М воспользуемся соотношением:
На заданной раме наметим расчётные сечения.
Рис.38
Построим эпюры моментов M1, M2 и M3 от найденных значений неизвестных («исправленные эпюры») (рис.39). Сложив эти эпюры с эпюрой Mр , получим окончательную эпюру моментов (рис.40). Результаты расчёта представим в табл.7.
Таблица 7
Номер сечения |
M1 |
M2 |
M3 |
Mр |
M |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
0,0224 |
0 |
7,0 |
6,25 |
13,27 |
3 |
0,0449 |
0 |
14,0 |
-7,5 |
6,55 |
4 |
-0,0299 |
0 |
7,0 |
0 |
6,97 |
5 |
0,12 |
1,424 |
0 |
-1,125 |
0,42 |
6 |
0,015 |
0 |
-7,0 |
0 |
-6,98 |
7 |
-0,015 |
-1,78 |
0 |
1,6875 |
-0,108 |
8 |
-0,06 |
-2,848 |
0 |
-3,375 |
-6,28 |
9 |
0 |
-0,712 |
7,0 |
0 |
6,28 |
10 |
0 |
0,356 |
-7,0 |
0 |
-6,64 |
Рис.39
Рис.40
Статическая проверка эпюры М на рис.41.
Рис.41
Дополнительно сделаем кинематическую проверку подобно тому, как это делается в методе сил (рис.42).
Рис.42 Основная система метода сил.
Следовательно, расчёт верный.
Эпюры Q и N строим так же, как в методе сил (рис.43).
Рис.43
Проверкой эпюр Q и N служит проверка равновесия сил для всей рамы (рис.44).
Рис.44
СПИСОК ЛИТЕРАТУРЫ:
Дарков А.В. Строительная механика: учебник для строительных специальностей вузов. – Изд. 10-е, с изм. – М.: Высш.шк., 2006
Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем). – Изд. 8-е, перераб. и доп. – М.: Высш. Шк., 2005.
Учебное издание
Составитель:
Грозин Дмитрий Александрович
Примеры расчёта статически неопределимых стержневых систем (часть II). Учебно-методическое пособие по курсу
«Строительная механика» для студентов
направления 270800 «Строительство»
Учебно-методическое пособие
В редакции составителя
Корректор
Подписано в печать. Формат 60×84/16
Усл. печ. л. 2,09. Тираж 100 экз. Заказ № 9
Издательство Ижевского государственного технического университета.
Отпечатано в типографии Издательства ИжГТУ. 426069, Ижевск, ул. Студенческая, 7