Задача №2. Расчёт неразрезной балки Методические рекомендации

Неразрезная балка загружена постоянной и временной нагрузками. Расчёт на постоянную нагрузку производится с помощью уравнений трёх моментов, на временную нагрузку – методом фокусных отношений. При решении задачи под заданной балкой необходимо изобразить основную систему метода сил, показать неизвестные опорные моменты и заданную постоянную нагрузку в пролётах. После решения уравнений трёх моментов полученные значения неизвестных надо обязательно подставить во все уравнения и убедится в правильности решения.

Эпюра моментов для неразрезной балки строится путём сложения грузовой эпюры с эпюрой опорных моментов. Проверка окончательной эпюры моментов выполняется обычным для метода сил путём. Так как единичные эпюры здесь однозначны, то можно сказать, что окончательная эпюра моментов на двух смежных пролётах не может быть однозначна. Не может быть однозначной и эпюра моментов в защемлённом одним концом пролёте. Построение эпюры поперечных сил производится по эпюре моментов.

Для построения эпюр моментов от попролётного загружения балки временной нагрузкой сначала необходимо вычислить моментные фокусные отношения (правые и левые) для каждого пролёта. Определение моментов на загруженном временной нагрузкой пролёте можно произвести по формулам (1):

(1)

где , - фиктивные опорные реакции от различных видов нагружения пролётов приводятся в таблице.

Для второго пролёта, для которого требуется строить объемлющую эпюру моментов, нужно определить ординаты окончательной эпюры в точках с интервалом . Ординаты объемлющей эпюры следует определять в табличной форме. При подсчёте максимального изгибающего момента для какого-либо сечения берётся момент от постоянной нагрузки и все положительные моменты от загружения отдельных пролётов временной нагрузкой; для минимального момента берётся момент от постоянной нагрузки и все отрицательные значения моментов от временной нагрузки. Соединяя последовательно ординаты и , получим объемлющие эпюры и .

Задание

Для неразрезной балки (рис. 16) с выбранными по шифру размерами и нагрузкой требуется:

1. Найти с помощью уравнений трёх моментов опорные моменты и построить эпюры M и Q от постоянной нагрузки (указанной на балке индексом 1).

2. Построить эпюры M и Q от временной нагрузки (указанной на балке индексом 2) методом фокусных отношений.

3. Построить объемлющую эпюру моментов для второго пролёта (считая слева).

Рис.16

Решение.

1. Определение степени статической неопределенности балки

,

где С_о – число опорных стержней.

2. Расчет на постоянную нагрузку с помощью уравнений трех моментов.

Рис.17

Составим уравнения трёх моментов для заданной балки, их будет по числу неизвестных моментов , , - три; момент на опоре 3 известен: кН·м.

(2)

Найдём значения

Пусть , тогда приведённые длины пролётов равны:

м; м; м

При равномерно распределённой нагрузке, пользуясь таблицей фиктивных опорных реакций, находим

Подставим найденные значения в уравнения (2):

Проведём преобразование:

В результате решения этих уравнений получим:

кН·м; кН·м; кН·м;

В каждом пролёте окончательную эпюру M строим как сумму найденных значений опорных моментов и эпюры для простых однопролётных балок основной системы. Эпюру Q строим также как сумму эпюр для однопролётных балок и эпюры Q от опорных моментов по формуле:

Максимальное значение момента в 1-м пролёте будет в сечении, где Q=0.

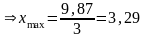, м

кН·м.

Эпюры M и Q, построенные по результатам подсчёта, приведены на рис.17.

После построения эпюры M выполняем кинематическую проверку правильности решения.

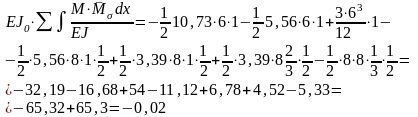Погрешность

По данным эпюры Q определяем опорные реакции:

Рис.18

кН; кН;

Выполняем статическую проверку правильности расчета балки:

3). Расчет балки на временную нагрузку методом фокусов.

Предварительно по формулам

и

Определим левые и правые фокусные отношения:

Расчет на нагрузку во 2-м пролете

Опорные моменты загруженного пролета находим по формуле (1):

По таблице фиктивных опорных реакций находим

кН·м

кН·м

Эпюры M и Q приведены на рис. 19. Определение опорных реакций показано на рис.20.

Рис. 19

Рис.20

Кинематическая проверка (эпюра , рис.17):

Статическая проверка:

Погрешность

Расчёт на нагрузку в 3-м пролёте кН/м.

Опорные моменты на концах загруженного пролёта найдём по формуле (1):

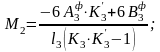
Учитываем, что Тогда имеем:

кН·м.

Эпюры M и Q приведены на рис.21. Определение опорных реакций показано на рис.22.

Рис.21

Рис.22

Кинематическая проверка (эпюра , рис.17):

Погрешность

Статическая проверка:

Построение объемлющей эпюры изгибающих моментов для второго пролёта.

Если кроме постоянной нагрузки имеется временная нагрузка, то бывает необходимо находить такое сочетание постоянной и временных нагрузок, которое вызывает в различных сечениях наибольшие и наименьшие изгибающие моменты.

Для определения максимального момента в данном сечении к моменту от постоянной нагрузки прибавляют все положительные моменты от временной нагрузки в данном сечении.

Для определения минимального момента в данном сечении к моменту от постоянной нагрузки прибавляют все отрицательные моменты от временной нагрузки :

Рассмотрим 2-й пролет. Определяем величину изгибающего момента в точках пролета а, б ,в с интервалом 0,25 при постоянной и временной нагрузке (рис. 23 )

Рис.23

Данные расчета представим в табличной форме.

Таблица 2

Номер сечения
1	-5,56	-3,375	8,01	2,45	-8,935
а	-3,32	2,555	-2,502	-0,765	-5,822
б	-1,08	8,48	-13,014	7,4	-14,094
в	1,15	2,414	-23,528	3,564	-22,378
2	3,39	-3,656	-34,04	3,39	-34,306

Строим объемлющие эпюры на одной базе (рис.24).

Рис.24